Trong không gian $\Large Oxyz$, cho hai mặt cầu $\Large (S_{1})$, $\La

Trong không gian $\Large Oxyz$, cho hai mặt cầu $\Large (S_{1})$, $\Large (S_{2})$ lần lượt có phương trình là $\Large x^{2} + y^{2} + z^{2} - 2x - 2y - 2z - 22 = 0$, $\Large x^{2} + y^{2} + z^{2} - 6x + 4y + 2z + 5 = 0$. Xét các mặt phẳng $\Large (P)$ thay đổi nhưng luôn tiếp xúc cả hai mặt cầu đã cho. Gọi $\Large M(a;b;c)$ là điểm mà tất cả các mặt $\Large (P)$ đi qua. Tính tổng $\Large S = a + b + c$.

 

 

• A.

  $\Large S = \dfrac{9}{2}$

• B.

  $\Large S = \dfrac{5}{2}$

• C.

  $\Large S = -\dfrac{5}{2}$

• D.

  $\Large S = -\dfrac{9}{2}$

Chọn D

Mặt cầu $\Large S_{1}$ có tâm $\Large I_{1}(1; 1; 1)$ và bán kính $\Large R_{1}=5$.

Mặt cầu $\Large S_{2}$ có tâm $\Large I_{2}(3; -2; -1)$ và bán kính $\Large R_{2}=3$.

Do $\Large I_{1}I_{2} = \sqrt{17} < R_{1} + R_{2}$ nên hai mặt cầu $\Large S_{1}$, $\Large S_{2}$ cắt nhau. Do vậy, mặt phẳng $\Large (P)$ tiếp xúc ngoài cả hai mặt cầu.

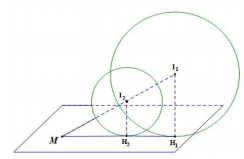
Giả sử $\Large (P)$ tiếp xúc với $\Large S_{1}$, $\Large S_{2}$ lần lượt tại $\Large H_{1}$, $\Large H_{2}$ và $\Large M = I_{1}I_{2} \cap (P)$.

Theo định lý Thalet, ta có:

$\Large \dfrac{MI_{2}}{MI_{1}} = \dfrac{I_{2}H_{2}}{I_{1}H_{1}} = \dfrac{3}{5}$

$\Large \Rightarrow \overrightarrow{MI_{2}} = \dfrac{3}{5}\overrightarrow{MI_{1}}$ (1).

Gọi $\Large M(a;b;c)$, khi đó từ (1) ta có:

$\Large \left\{\begin{array}{l}3 - a = \dfrac{3}{5}(1 - a) \\- 2 - b = \dfrac{3}{5}(1 - b) \\-1 - c = \dfrac{3}{5}(1 - c)\end{array}\right.$

$\Large \Leftrightarrow \left\{\begin{array}{l} a = 6 \\ b = -\dfrac{13}{2}\\ c = -4\end{array}\right.$

Suy ra, các mặt phẳng $\Large (P)$ đều đi qua điểm $\Large M(6;-\dfrac{13}{2};-4)$

và $\Large a + b + c = -\dfrac{9}{2}$.