Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh $\Large a$ . Cạnh bên $\Large SA = a$ và vuông góc với mặt phẳng đáy. Gọi $\Large M,N$ lần lượt là trung điểm của $\Large SC$ và $\Large AB$ . Khoảng cách từ $\Large M$ đến đường thẳng $\Large CN$ bằng

• A.

  $\Large \dfrac{a\sqrt{30}}{10}$

• B.

  $\Large \dfrac{a\sqrt{10}}{10}$

• C.

   $\Large \dfrac{a\sqrt{3}}{2}$

• D.

   $\Large \dfrac{2a\sqrt{5}}{5}$

Chọn A

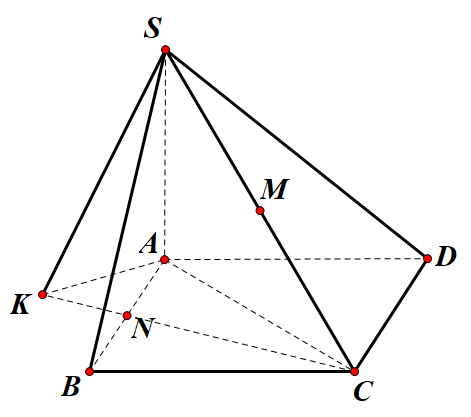
Ta có:

$\Large \dfrac{d(M; CN)}{d(S;CN)} = \dfrac{MC}{SC} = \dfrac{1}{2}$

$\Large d(M; CN) = \dfrac{1}{2}d(S;CN)$

Kẻ $\Large AK \bot CN$ ($\Large K \in CN$)

$\Large \begin{cases}CN \bot SA \\CN \bot AK\end{cases}$

$\Large \Rightarrow CN \bot (SAK)$

$\Large \Rightarrow CN \bot SK$

$\Large \Rightarrow d(S; CN) = SK$.

Ta có:

$\Large S_{\Delta ANC} = \dfrac{1}{2}S_{\Delta ABC}$

$\Large \Leftrightarrow AK . NC = \dfrac{1}{2}AB. BC$

$\Large AK = \dfrac{AB.BC}{2CN} = \dfrac{a.a}{2a\dfrac{\sqrt{5}}{2}} = \dfrac{a}{\sqrt{5}}$

Xét tam giác $\Large SAK$ vuông tại $\Large A$ ta có:

$\Large SK^{2} = SA^{2} + AK^{2} = a^{2} + \left ( \dfrac{a}{\sqrt{5}} \right )^{2} = \dfrac{6a^{2}}{5}$

$\Large \Rightarrow SK = \dfrac{a\sqrt{30}}{5}$

$\Large \Rightarrow d(M; CN) = \dfrac{1}{2}SK = \dfrac{a\sqrt{30}}{10}$.