Hình vẽ bên dưới là đồ thị hàm số $\Large y = f(x)$ Gọi $\Large S$ là

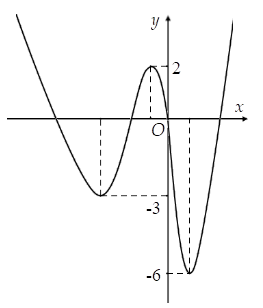
Hình vẽ bên dưới là đồ thị hàm số $\Large y = f(x)$

Gọi $\Large S$ là tập hợp các số nguyên dương của tham số $\Large m$ để hàm số $\Large y = \left | f(x - 1) + m \right |$ có 5 điểm cực trị. Phần tử lớn nhất của tập hợp $\Large S$ là

• A.

  7. 

• B.

  6. 

• C.

  4. 

• D.

  5.

Chọn D

Từ đồ thị hàm số $\Large y =f(x)$ suy ra $\Large y =f(x)$ có 3 điểm cực trị nên hàm số $\Large y = f(x - 1) + m$ có 3 điểm cực trị.

Do đó đồ thị hàm số $\Large y = \left | f(x - 1) + m \right |$ có 5 điểm cực trị khi và chỉ khi đồ thị hàm số $\Large y = f(x - 1) + m$ cắt trục hoành tại hai điểm phân biệt hoặc phương trình $\Large f(x - 1) + m = 0$ có 3 nghiệm phân biệt trong đó có 1 nghiệm kép

$\Large \Leftrightarrow \left[\begin{array}{l}3 \leq m < 6 \\m \leq -2 \\\end{array}\right.$

$\Large \Rightarrow S = {3; 4; 5}$ do $\Large S \subset \mathbb{Z}^{*}_{+}$.

Vậy phần tử lớn nhất của $\Large S$ là 5.