Cho hình chóp $\Large S.ABCD$ có đáy là hình vuông cạnh $\Large a$, $\

Cho hình chóp $\Large S.ABCD$ có đáy là hình vuông cạnh $\Large a$, $\Large SAD$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $\Large E, F$ lần lượt là trung điểm của $\Large BC$ và $\Large CD$. Tính bán kính $\Large R$ của mặt cầu ngoại tiếp hình chóp $\Large S.CEF$.

• A.

  $\Large R = \dfrac{a\sqrt{93}}{12}$

• B.

  $\Large R = \dfrac{a\sqrt{29}}{8}$

• C.

   $\Large R = \dfrac{5a\sqrt{3}}{12}$

• D.

  $\Large R = \dfrac{a\sqrt{37}}{6}$

Chọn A

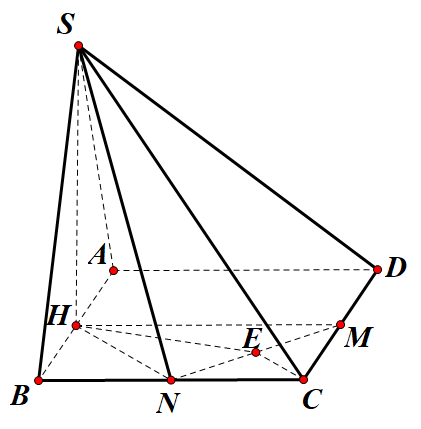
Gọi $\Large E$ là trung điểm $\Large MN$

$\Large \Rightarrow E$ là tâm đường tròn ngoại tiếp tam giác $\Large CMN$ và:

$\Large r = CE = \dfrac{MN}{2} = \dfrac{BD}{4} = \dfrac{a\sqrt{2}}{4}$ là bán kính đường tròn ngoại tiếp tam giác $\Large CMN$.

Ta có:

$\Large HE^{2} = \dfrac{HM^{2} + HN^{2}}{2} - \dfrac{MN^{2}}{4} = \dfrac{5a^{2}}{8}$

$\Large SE^{2} = SH^{2} + HE^{2} = \left ( \dfrac{a\sqrt{3}}{2} \right )^{2} + \dfrac{5a^{2}}{8} = \dfrac{11a^{2}}{8}$

Khi đó, ta có:

$\Large R = \sqrt{\left ( \dfrac{SE^{2}-CE^{2}}{2SH} \right )^{2} + CE^{2}} = \sqrt{\left ( \dfrac{\dfrac{11a^{2}}{8} - \dfrac{a^{2}}{8}}{2.\dfrac{a\sqrt{3}}{2}} \right )^{2} + \dfrac{a^{2}}{8}} =  \dfrac{a\sqrt{93}}{12}$.