Cho khối lăng trụ $\Large ABC.A’B’C’$ có thể tích bằng $\Large 1$. Gọi

Cho khối lăng trụ $\Large ABC.A’B’C’$ có thể tích bằng $\Large 1$. Gọi $\Large M$,$\Large N$ lần lượt là trung điểm của các đoạn thẳng $\Large AA’$ và $\Large BB’$ . Đường thẳng $\Large CM$ cắt đường thẳng $\Large C’A’$ tại $\Large P$ , đường thẳng $\Large CN$ cắt đường thẳng $\Large C’B’$ tại  $\Large Q$. Thể tích khối đa diện lồi  $\Large  A’MPB’NQ$ bằng 

• A.

  $\Large 1$.

• B.

  $\Large \dfrac{1}{2}$.

• C.

  $\Large \dfrac{2}{3}$.

• D.

  $\Large \dfrac{1}{3}$.

Chọn C

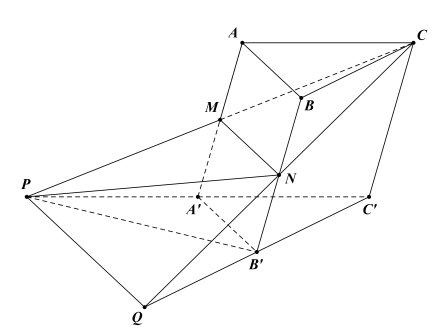
Đặt thể tích khối lăng trụ $\Large ABC.A’B’C’$ là $\Large V$ $\Large \Rightarrow V =1$.

Ta có:$\Large V_{A'MPB'NQ} =V_{P.MNB'A'} + V_{P.QNB'} \left ( 1 \right )$.

Lại có:  $\Large V_{P.MNB'A'} =V_{C'MNB'A'}=\frac{1}{2}V_{C'AA'B'B}=\frac{1}{2}.\frac{2}{3}V=\frac{1}{3}V=\frac{1}{3} \left ( 2 \right )$.

Mặt khác: $\Large d\left ( P,\left ( BB'C'C \right ) \right )=2d\left ( A',\left ( BB'C'C \right ) \right )$ và $\Large S_{\Delta QNB'} = S_{\Delta CNB} = \dfrac{1}{4}S_{BB{}'C{}'C}$.

Nên:

$\Large V_{P.QNB{}'}  = \dfrac{1}{2}V_{A{}'.BB{}'C{}'C} = \dfrac{1}{3}V = \dfrac{1}{3}$ (3)

Từ (1), (2) và (3) suy ra:

$\Large V_{A{}'MPB{}'NQ} = V_{P.MNB{}'A{}'} + V_{P.QNB{}'} = \dfrac{2}{3}$