Trong không gian $\Large Oxyz$, cho hai điểm A(10;6;-2), B(5;10;-9) và

Trong không gian $\Large Oxyz$, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng $\Large (\alpha):2x+2y+z-12=0$. Điểm M di động trên $\Large (\alpha)$ sao cho MA, MB luôn tạo với $\Large (\alpha)$ các góc bằng nhau. Biết bằng M luôn thuộc một đường tròn $\Large (\omega)$ cố định. Hoành độ của tâm đường tròn $\Large (\omega)$ bằng

• A. -4
• B. $\Large \dfrac{9}{2}$
• C. 2
• D. 10

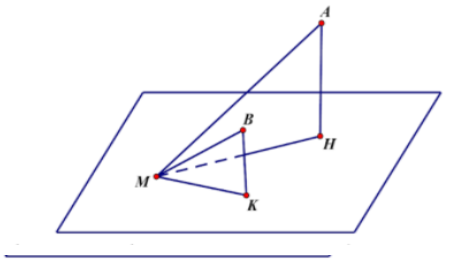
Gọi H, K lần lượt là hình chiếu vuông góc của A, B trên mặt phẳng $\Large (\alpha)$, khi đó:

$\Large AH=d(A;(\alpha))=\dfrac{|2.10+2.6+(-2)-12|}{\sqrt{2^{2}+2^{2}+1^{2}}}=6$

$\Large BK=d(B;(\alpha))=\dfrac{|2.5+2.10+(-9)-12|}{\sqrt{2^{2}+2^{2}+1^{2}}}=3$

Vì MA, MB với $\Large (\alpha)$ các góc bằng nhau nên $\Large \widehat{AMH}=\widehat{BMK}$. Từ AH = 2BK suy ra MA = 2MB

Gọi M(x;y;z), ta có: 

$\Large MA=2MB\Leftrightarrow MA^{2}=4MB^{2}$

$\Large \Leftrightarrow (x-10)^{2}+(y-6)^{2}+(z+2)^{2}=4[(x-5)^{2}+(y-10)^{2}+(z+9)^{2}]$

$\Large \Leftrightarrow x^{2}+y^{2}+z^{2}-\dfrac{20}{3}x-\dfrac{68}{3}y+\dfrac{68}{3}z+228=0$

Như vậy, điểm M nằm trên mặt cầu (S) có tâm $\Large I\left(\dfrac{10}{3};\dfrac{34}{3};\dfrac{34}{3}\right)$ và bán kính $\Large R=2\sqrt{10}$. Do đó, đường tròn $\Large (\omega)$ là giao của mặt cầu $\Large (S)$ và mặt phẳng $\Large (\alpha)$, nên tâm J của đường tròn D là hình chiếu vuông góc của I trên mặt phẳng $\Large (\alpha)$

Phương trình đường thẳng d đi qua I và vuông góc với mặt phẳng $\Large (\alpha)$ là: $\Large \left\{\begin{align}&x=\dfrac{10}{3}+2t\\&y=\dfrac{34}{3}+2t\\&z=-\dfrac{34}{3}+t\\\end{align}\right.$

Tọa độ điểm J là nghiệm (x;y;z) của hệ phương trình: $\Large \left\{\begin{align}&x=\dfrac{10}{3}+2t\\&y=\dfrac{34}{3}+2t\\&z=-\dfrac{34}{3}+t\\&2x+2y+z-12=0\\\end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align}&x=2\\&y=10\\&z=-\dfrac{38}{3}\\&t=-\dfrac{2}{3}\\\end{align}\right.$

Vậy $\Large J=\left(2;10;-\dfrac{38}{3}\right)$