Trong không gian, cho hình thang ABCD vuông tại A và D, cạnh đáy AB =
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Trong không gian, cho hình thang ABCD vuông tại A và D, cạnh đáy AB = 5a và AD = CD = 2a. Thể tích khối tròn xoay tạo thành khi quay hình thang ABCD quanh cạnh đáy CD bằng
Đáp án án đúng là: D
Lời giải chi tiết:
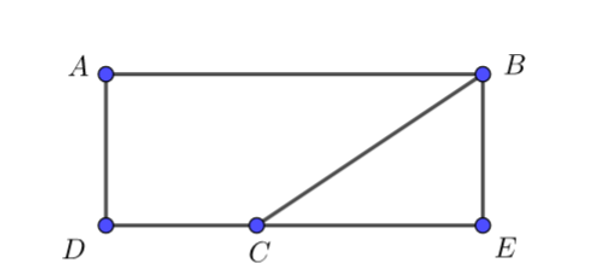
Hạ BE⊥CD(E∈CD).
Gọi thể tích khối tròn xoay khi quay ABCD, ABED, BEC quanh CD lần lượt là V1,V2,V3.
Có V1=V2−V3
V2 là thể tích hình trụ có h=DE=5a,r=AD=2a⇔V2=π.DE.AD2=20πa3
V3 là thể tích hình nón có h=CE=3a,r=BE=2a⇔V3=13π.CE.BE2=4πa3
V1=V2−V3=20πa3−4πa3=16πa3
Xem thêm các bài tiếp theo bên dưới