Trong không gian, cho hình chữ nhật ABCD có AB = a, AC = 2a . Khi quay

Trong không gian, cho hình chữ nhật ABCD có AB = a, AC = 2a . Khi quay hình chữ nhật ABCD quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung  quanh của hình trụ đó bằng
 

• A.

  $\large 4 \pi a^{2}$

• B.

  $\large \pi a^{2} \sqrt {3}$

• C.

  $\large 2 \pi a^{2} \sqrt {5}$

• D.

  $\large 2 \pi a^{2} \sqrt {3}$

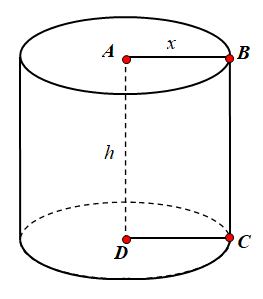
Ta có ABCD là hình chữ nhật có AB = a, AC = 2a suy ra $\large AD = \sqrt {AC^{2} - AB^{2}} = a \sqrt {3}$
Hình trụ $\large h = l = AD = a \sqrt {3}; r = a = AB = a$
Diện tích xung quanh của hình trụ là $\large S_{xq} = 2 \pi r l = 2 \pi a.a. \sqrt {3} = 2 \pi a^{2} \sqrt {3}$