Cho hình lăng trụ đứng $\large ABC.A^{'} B^{'}C^{'}$ có đáy ABC là tam

Cho hình lăng trụ đứng $\large ABC.A^{'} B^{'}C^{'}$ có đáy ABC là tam giác vuông tại B, $\large AB = a \sqrt {3}, BC = 2a, AA^{'} = a \sqrt {2}$. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B'C

• A.

  $\large \dfrac {a \sqrt {10}}{10}$

• B.

  $\large 2a$

• C.

  $\large a \sqrt {2}$

• D.

  $\large \dfrac {a \sqrt {30}}{10}$

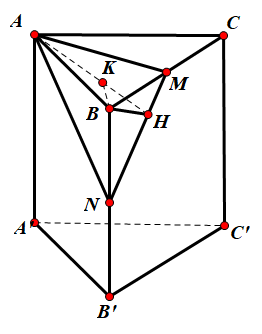
Gọi N là trung điểm $\large BB', B'C // MN \to B'C // (AMN)$
$\large \to d(AM, B'C) = d(B'C, (AMN)) = d(B', (AMN)) =  d(B, (AMN))$
Kẻ $\large BH \perp MN,  BK \perp AH \to d(B, (AMN)) = BK$ 
Ta có $\large \dfrac {1}{BK^{2}} = \dfrac {1}{BA^{2}} + \dfrac {1}{BM^{2}} + \dfrac {1}{BN^{2}} = \dfrac {1}{3a^{2}} + \dfrac {1}{a^{2}} + \dfrac {2}{a^{2}} = \dfrac {10}{3a^{2}} \to BK = \dfrac {a \sqrt {30}}{10}$