Cho hàm số $\large y = ax^{3} + bx^{2} + x + c (a, b, c \in \mathbb{R}

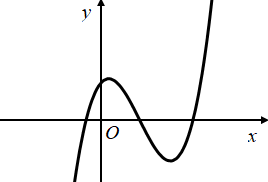
Cho hàm số $\large y = ax^{3} + bx^{2} + x + c (a, b, c \in \mathbb{R})$ có đồ thị như hình sau

• A.

  $\large a > 0; b > 0; c > 0$

• B.

  $\large a > 0; b < 0; c > 0$

• C.

  $\large a < 0; b < 0; c < 0$

• D.

  $\large a < 0; b > 0; c > 0$

Từ đồ thị suy ra $\large a > 0; c > 0$
Với mọi $\large x \in \mathbb{R}$ $\large y' = 3ax^{2} + 2bx + 1$, pt $\large y' = 0$ có 2 nghiệm $\large x_{1}, x_{2}$ sao cho $\large \left\{\begin{matrix} x_{1} + x_{2} = - \dfrac {2b}{3a} > 0 \\ x_{1} . x_{2} = \dfrac {1}{3a} > 0 \end{matrix}\right. \to b < 0$