Cho lăng trụ tam giác đều $\large ABC.A'B'C'$ có độ dài cạnh đáy bằng

Cho lăng trụ tam giác đều $\large ABC.A'B'C'$  có độ dài cạnh đáy bằng $\large a$ . Gọi $\large \varphi $ là góc giữa BC' và mặt phẳng (A'BC). Khi $\large sin \varphi$ đạt giá trị lớn nhất, tính thể tích khối trụ đã cho

• A.

  $\large \dfrac {\sqrt {6} a^{3}}{4}$

• B.

  $\large \dfrac {\sqrt {3} a^{3}}{4}$

• C.

  $\large \dfrac { \sqrt[4]{12} a^{3}}{4 \sqrt {3}}$

• D.

  $\large \dfrac { \sqrt[4]{27} a^{3}}{4 \sqrt {2}}$

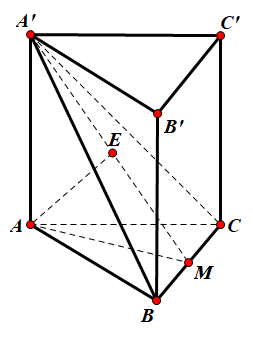
Đặt $\large AA' = x (x > 0)$
Gọi $\large h = d(A, (A'BC)) = d(C', (A'BC))$
Dựng $\large AM \perp BC, AE \perp A'M$$\Large  \Rightarrow h = d(A, (A'BC)) = d(C', (A'BC)) = AE = \dfrac {A'A.MA}{\sqrt {A'A^{2} + AM^{2}}}$
Khi đó ta có $\large h = \dfrac {a \sqrt {3} x}{\sqrt {4x^{2} + 3a^{2}}}$ và $\large BC' = \sqrt {x^{2} + a^{2}} $
Ta có: $\large sin \varphi = \dfrac {h}{BC'} = \dfrac {a \sqrt {3} x}{\sqrt {4x^{2} + 3a^{2}} \sqrt {x^{2} + a^{2}}} = \dfrac {a \sqrt {3}}{\sqrt {\dfrac {(4x^{2} + 3a^{2})(x^{2} + a^{2})}{x^{2}}}}$
Ta có $\large sin \varphi$ lớn nhất khi $\large \dfrac {(4x^{2} + 3a^{2})(x^{2} + a^{2})}{x^{2}}$ nhỏ nhất 
Mà $\large \dfrac {(4x^{2} + 3a^{2})(x^{2} + a^{2})}{x^{2}} = 4x^{2} + \dfrac {3a^{4}}{x^{2}} + 7a^{2} \geq 4a^{2} \sqrt {3} + 7a^{2}$

Dấu "=" xảy ra khi $\large 4x^{2} = \dfrac {3a^{4}}{x^{2}} \Rightarrow x = a \sqrt[4]{\dfrac {3}{4}}$, khi đó thể tich khối lăng trụ bằng $\large V=h. S_{ABC}= \dfrac { \sqrt[4]{27} a^{3}}{4 \sqrt {2}}$