Cho hình lăng trụ tam giác đều $\large ABC.A'B'C'$ có chiều cao bằng 4

Cho hình lăng trụ tam giác đều $\large ABC.A'B'C'$  có chiều cao bằng 4 cm và diện tích đáy bằng 6 $\large cm^{2}$. Gọi M, N, P  lần lượt là trung điểm của các cạnh  AB, BB', A'C'. Thể tích của khối tứ diện CMNP bằng

• A.

  $\large 7 cm^{3}$

• B.

  $\large \dfrac {7}{2} cm^{3}$

• C.

  $\large 8 cm^{3}$

• D.

  $\large 5 cm^{3}$

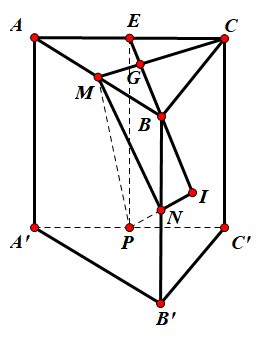
Gọi E là trung điểm của AC
Khi đó: $\large PE // BB'$ 
Gọi I là giao điểm của NP và BE, khi đó B là trung điểm của IE. Gọi G là trọng tâm của tam giác ABC
Theo tính chất của trọng tâm: BG = 2EG
Ta được: $\large d (B;MC) = 2d (E;MC)$
$\large IB = BE = \dfrac {3}{2} BG $
Suy ra $\large d (I; MC) = \left(1 + \dfrac {3}{2} \right)d (B;MC)  = \dfrac {5}{2} d (B;MC)$
$\large S_{IMC} =  \dfrac {1}{2} d (I;MC) . MC = \dfrac {1}{2} . \dfrac {5}{2} d (B;MC) . MC = \dfrac {5}{2} S_{MBC} = \dfrac {5}{4} S_{ABC}$
Ta có: $\large \dfrac {V_{P.MNC}}{V_{P.MIC}} = \dfrac {1}{2} \Rightarrow V_{P.MNC} = \dfrac {1}{2} V_{P.MIC}$
Lại có $\large  V_{P.MIC} = \dfrac {1}{3} d (P;(ABC)) . S_{MIC} = \dfrac {1}{3} d (A';(ABC)) . \dfrac {5}{4} S_{ABC}$
$\large \Rightarrow V_{P.MIC} = \dfrac {1}{3} d (A';(ABC)) . \dfrac {5}{4} S_{ABC} = \dfrac {5}{12} . 4.6 = 10 (cm^{3})$
Vậy $\large V_{P.MNC} = \dfrac {1}{2} V_{P.MIC} = 5 (cm^{3})$