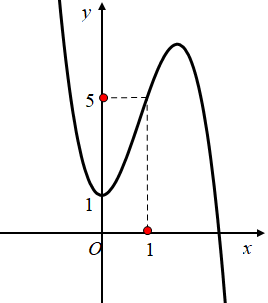
Cho đa thức bậc ba $\large y = f(x)$ có đồ thị hàm số như hình vẽ sau

Cho đa thức bậc ba $\large y = f(x)$ có đồ thị hàm số như hình vẽ sau

Có bao nhiêu giá trị nguyên của tham số $\large m$ sao cho phương trình 
$\large 8^{f(x) - 1} + 4^{f(x) - 1} - (m +3).2^{f(x)} + 4 + 2m = 0$ có nghiệm $\large x \in (0;1)$

• A.

  285

• B.

  284

• C.

  141

• D.

  142

Đặt $\large 2^{f(x) - 1} = a $
Vì $\large x \in (0;1) \to f(x) \in (1;5) \to a \in (1;16)$
Phương trình $\large a^{3} + a^{2} - 2(m + 3)a + 2m + 4 = 0 \Leftrightarrow  (a - 1)(a^{2} + 2a - (2m + 4)) = 0 \Leftrightarrow  a = 1$ (vô nghiệm) và $\large a^{2} + 2a = 2m + 4 \Leftrightarrow  (a + 1)^{2} = 2m + 5 \Leftrightarrow \left\{\begin{matrix} m \in \mathbb{Z} \\ m \in (- \dfrac {1}{2};142) \end{matrix}\right.$
Vậy có 142 số