Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2; 3; 3; 2 (đ

Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2; 3; 3; 2 (đơn vị độ dài) đôi một tiếp xúc nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng:

• A. A. $\large \dfrac{7}{15}$
• B. B. $\large \dfrac{3}{7}$
• C. C. $\large \dfrac{6}{11}$
• D. D. $\large \dfrac{5}{9}$

Chọn C

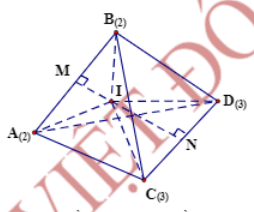
* Gọi A, B lần lượt là tâm của hai mặt cầu có bán kính bằng 2; C, D lần lượt là tâm của hai mặt cầu có bán kính bằng 3 và I là tâm mặt cầu cần tìm với bán kính bằng x (x > 0).

* Mặt cầu (I) tiếp xúc ngoài với bốn mặt cầu tâm A, B, C, D 
$\large \Leftrightarrow \left\{\begin{matrix} IA = IB = x+2 & \\  IC = ID = x+3 &  \end{matrix}\right.$ 

* IA = IB $\large \Leftrightarrow I \in$ mp (P) là mặt phẳng trung trực của đoạn AB và IC = ID $\large \Leftrightarrow I \in$ (Q) là mặt phẳng trung trực của đoạn CD. Suy ra: $\large I \in (P)\cap (Q)$   (1)

* Tứ diện ABCD có DA = DB = CA = CB = 5 nên nếu gọi M, N lần lượt là trung điểm của AB và CD thì MN là đường vuông góc chung của AB và CD $\large \Rightarrow MN \subset (P)$ và $\large MN \subset$ (Q).

Suy ra $\large MN = (P)\cap (Q)$ (2). Từ (1) và (2) suy ra $\large I \in MN$.

Xét $\large \Delta AIM$ có $\large IM = \sqrt{IA^{2}-AM^{2}} = \sqrt{(x+2)^{2}-4}$ và $\large \Delta CIN$ có:

$\large IN = \sqrt{IC^{2}-CN^{2}} = \sqrt{(x+3)^{2}-9}$.

Ta có: 

$\large MN = \sqrt{AN^{2}-AM^{2}} = \sqrt{\left (\dfrac{AC^{2}+AD^{2}}{2}-\dfrac{CD^{2}}{4}  \right )-4} = \sqrt{\left (\dfrac{5^{2}+5^{2}}{2}-\dfrac{6^{2}}{4}  \right )-4} = \sqrt{12}$ 

* Mà IM+IN = MN $\large \Leftrightarrow \sqrt{(x+2)^{2}-4}+\sqrt{(x+3)^{2}-9} = \sqrt{12} \Leftrightarrow \sqrt{x^{2}+4x} = \sqrt{12}-\sqrt{x^{2}+6x}$ 

$\large \Rightarrow x^{2}+4x = 12+x^{2}+6x-2\sqrt{12(x^{2}+6x)}\Leftrightarrow \sqrt{12(x^{2}+6x)} = x+6 = 11x^{2}+60x-36 = 0$ 

* Thử lại x = -6(l); x = $\large \dfrac{6}{11}$ (nhận).