Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) bằng 60∘. Gọi G là trọng tâm tam giác SAC, R là bán kính mặt cầu có tâm G và tiếp xúc với mặt phẳng (SAB). Đẳng thức nào sau đây sai?
Đáp án án đúng là: D
Lời giải chi tiết:
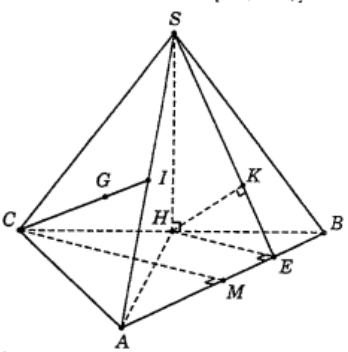
Ta có 60∘=^SA,(ABC=^SA,HA=^SAH
Tam giác ABC đều cạnh a nên AH=a√32
Trong tam giác vuông SHA, ta có SH=AH.tan^SAH=3a2
Vì mặt cầu có tâm G và tiếp xúc với (SAB) nên bán kính mặt cầu R = d[G,(SAB)].
{CM⊥ABCM=a√32 và {HE⊥ABHE=12CM=a√34
Gọi K là hình chiếu vuông góc của H trên SE, suy ra HK⊥SE (1)
Ta có {HE⊥ABAB⊥SH⇒AB⊥(SHE)⇒AB⊥HK. (2)
Từ (1) và (2), suy ra HK⊥(SAB) nên d[H,(SAB)] = HK.
Trong tam giác vuông SHE, ta có HK=SH.HE√SH2+HE2=3a2√13
Vậy R=23HK=a√13. Chọn D.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc $\large \wi
- Cho tứ diện ABCD có DA vuông góc với mp( ABC ), DB⊥BC ,
- Thể tích V của khối tròn xoay thu được khi quay hình thang ABCD quanh
- Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đườn
- Cho một hình trụ có bán kính đáy R = 5, chiều cao h = 6. Một đoạn thẳn