Trong hệ tọa độ Oxyz , cho điểm A(2;1;3) , mặt phẳng $\large (\alpha):

Trong hệ tọa độ Oxyz , cho điểm A(2;1;3) , mặt phẳng $\large (\alpha): 2x + 2 y - z - 3 = 0$ và mặt cầu $\large (S): x^{2} + y^{2} + z^{2} - 6x - 4 y -10z + 2 = 0$. Gọi D là đường thẳng đi qua A , nằm trong mặt phẳng $\large (\alpha)$ và cắt $\large (S)$ tại hai điểm M, N. Độ dài đoạn MN nhỏ nhất là:

• A.

  $\large 2 \sqrt {30}$

• B.

  $\large \sqrt {30}$

• C.

  $\large  \dfrac {\sqrt {30}}{2}$

• D.

  $\large  \dfrac {3 \sqrt {30}}{2}$

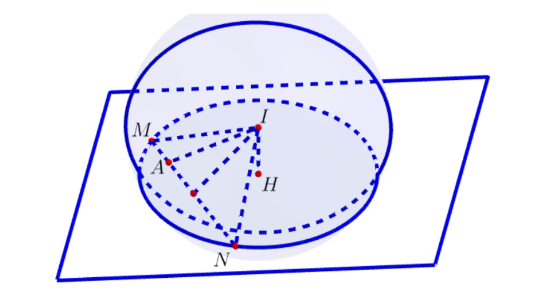
Mặt cầu $\large (S)$ có tâm I(3;2;5) và bán kính R = 5
Ta có: $\large A  \in (\alpha)$, $\large IA = \sqrt {6} < R$ nên $\large (S) \cap  (\alpha) = (C)$ và A nằm trong mặt cầu $\large (S)$. 
Suy ra: Mọi đường thẳng $\large \Delta$ đi qua A , nằm trong mặt phẳng $\large (\alpha)$ đều cắt $\large (S)$ tại hai điểm M, N. (M, N cũng chính là giao điểm của $\large \Delta$ và (C)).
Vì $\large d(I; \Delta) \leq IA$ nên ta có $\large MN = 2 \sqrt {R^{2} - d^{2}(I; \Delta)} \geq 2 \sqrt {R^{2} - IA^{2}} = 2 \sqrt {30}$
Dấu "=" xảy ra khi A là điểm chính giữa cung MN
Vậy độ dài đoạn MN nhỏ nhất là MN bằng $\large 2 \sqrt {30}$