Tập hợp tất cả các giá trị thực của tham số $\large m$ để hàm số $\lar

Tập hợp tất cả các giá trị thực của tham số $\large m$ để hàm số $\large y = ln(x^{2} +4) + mx + 12$ đồng biến trên $\large \mathbb{R}$ là

• A.

  $\large \left[\dfrac {1}{2}; + \infty\right)$

• B.

  $\large \left(- \dfrac {1}{2}; \dfrac {1}{2}\right)$

• C.

  $\large \left(- \infty;- \dfrac {1}{2}\right]$

• D.

  $\large \left(\dfrac {1}{2}; + \infty\right)$

+ TXĐ: $\large \mathbb{R}$
+ Ta có: $\large y' = \dfrac {2x}{x^{2} + 4} + m$. Hàm số đồng biến trên $\large \mathbb{R} \Leftrightarrow  \dfrac {2x}{x^{2} + 4} + m \geq 0$, với mọi $\large x \in \mathbb{R}$
$\large \Leftrightarrow m\geq  \dfrac {-2x}{x^{2} + 4}$ với mọi $\large x \in \mathbb{R}$
Xét $\large f(x) = \dfrac {-2x}{x^{2} + 4}$. Ta có: $\large f'(x) = \dfrac {2(x^{2} - 4)}{x^{2} + 4)} = 0 \Leftrightarrow x = \pm 2$
Bảng biến thiên 

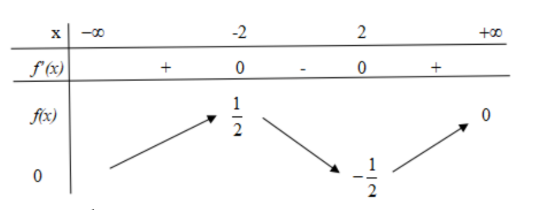
Vậy giá trị cần tìm là $\large m > \dfrac {1}{2}$