Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông, tam giác SAB đề

Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của cạnh CD. Biết khoảng cách từ A đến (SBM) là $\large 2a \sqrt {\dfrac {3}{19}}$. Thể tích khối chóp SABCD bằng

• A.

  $\large \dfrac {\sqrt {3} a^{3}}{6}$

• B.

  $\large \sqrt {3} a^{3}$

• C.

  $\large \dfrac {\sqrt {3} a^{3}}{12}$

• D.

  $\large \dfrac {2 \sqrt {3} a^{3}}{18}$

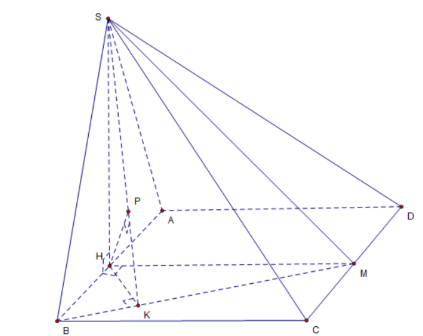
Gọi H là trung điểm của $\large AB \Leftrightarrow SH \perp AB \Leftrightarrow (SH) \perp (ABCD)$ (Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy).
Ta có: $\large AB = 2HB \Leftrightarrow d(A,(SBM)) = 2d (H, (SBM))$. 
Từ H kẻ $\large HK \perp BM \Leftrightarrow BM \perp (SHK) \Leftrightarrow (SHK) \perp (SBM)$ mà $\large (SHK) \cap  (SBM) = SK$
$\large HP \perp SK \Rightarrow  HP \perp (SBM) \Rightarrow  d (H, (SBM)) = HP \Rightarrow  HP = a \sqrt {\dfrac {3}{19}}$.
Giả sử hình vuông ABCD có độ dài cạnh là x ( x > 0) .
$\large \Leftrightarrow \Delta SAB$ đều cạnh $\large \Leftrightarrow SH = \dfrac {x \sqrt {3}}{2}$
$\large BM = \sqrt {BC^{2} + CM^{2}} = \dfrac {x \sqrt {5}}{2}$
Trong $\large \Delta BHM$ vuông tại H có $\large HK.BM = HB.HM \Leftrightarrow HK = \dfrac {HB.HM}{MB} = \dfrac {x \sqrt {5}}{5}$
$\large \Delta SHK$ có $\large \dfrac {1}{HP^2} = \dfrac {1}{HS^{2}} + \dfrac {1}{HK^{2}} \Leftrightarrow x = a$
Vậy $\large V_{S.ABCD} = \dfrac {1}{3} SH . S_{ABCD} = \dfrac {\sqrt {3} a^{3}}{6}$