Cho hàm số $\large y = f(x)$ có đạo hàm liên tục trên $\large \mathbb{

Cho hàm số $\large y = f(x)$ có đạo hàm liên tục trên $\large \mathbb{R}$ và có đồ thị $\large y = f'(x)$ như hình vẽ. Đặt  $\large g(x) = f(x - m) - \dfrac {1}{2} (x - m - 1)^{2} + 2019$ với $\large m$ là tham số thực. Gọi $\large S$ là tập hợp các giá trị  nguyên dương của $\large m$ để hàm số $\large y = g (x)$ đồng biến trên khoảng (5;6). Tổng tất cả các phần tử trong $\large S$ bằng

• A.

  4

• B.

  11

• C.

  14

• D.

  20

Xét hàm số $\large g(x) = f(x - m) - \dfrac {1}{2} (x - m - 1)^{2} + 2019$
$\large g'(x) = f'(x - m) - (x - m -1)$
Xét phương trình $\large g'(x) = 0$ (1)
Đặt $\large x - m = t$, phương trình (1) trở thành $\large g'(x) = f'(t) - (t - 1)$ (2)
Nghiệm phương trình (2) là hoành độ giao điểm của hai đồ thị hàm số $\large y = f(t)$ và $\large y = t - 1$
Ta có đồ thị các hàm số $\large y = f'(t)$ và $\large y = t - 1$ như sau  

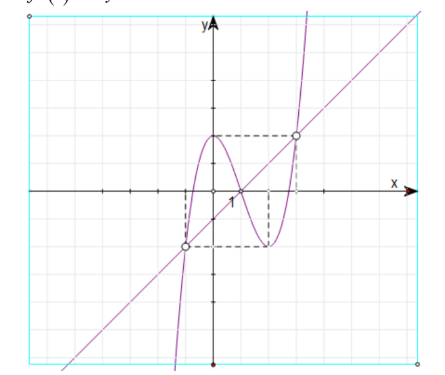
Căn cứ đồ thị các hàm số ta có phương trình (2) có nghiệm là: $\large \Leftrightarrow \left[\begin{align} &t = -1 \\ &t = 1 \\ &t = 3 \end{align}\right.$ $\large \Leftrightarrow \left[\begin{align} &x = m - 1 \\ &x = m + 1 \\ &x = m + 3 \end{align}\right.$
Ta có bảng biến thiên $\large y = g(x)$

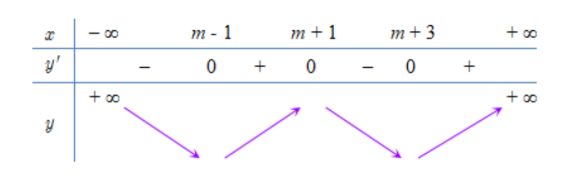
Để hàm số $\large y = g(x)$ đồng biến trên khoảng (5;6) cần $\large \Leftrightarrow \left[\begin{align} & \left\{\begin{matrix} m - 1 \leq 5 \\ m + 1 \geq 6 \end{matrix}\right. \\ &m + 3 \leq 5 \end{align}\right.$ $\large \Leftrightarrow \left[\begin{align} &5 \leq m \leq 6 \\ &m \leq 2 \end{align}\right.$
Vì $\large m \in \mathbb{N^{*}} \Rightarrow m$ nhận các giá trị $\large \{1;2;5;6\} \Rightarrow S = 14$