Trên một sợi dây đàn hồi dài 1,2 m với hai đầu cố định, đang có sóng d

Trên một sợi dây đàn hồi dài 1,2 m với hai đầu cố định, đang có sóng dừng với 5 nút sóng (kể cả hai đầu dây). Gọi M và N là hai điểm gần nhất trên dây mà phần tử M và N có cùng biên độ dao động và bằng nửa biên độ dao động của bụng sóng. Khoảng cách giữa vị trí cân bằng của hai điểm M và N bằng

• A. A. 30 cm.
• B. B. 20 cm.
• C. C. 40 cm.
• D. D. 10 cm.

Phương pháp: 
Điều kiện có sóng dừng  $\large l=k.\dfrac{\lambda}{2}$ với k là số bó sóng
Biên độ của điểm cách nút gần nhất khoảng d: $\large a=2a_0.\sin\dfrac{2\pi d}{\lambda}$
Cách giải: 

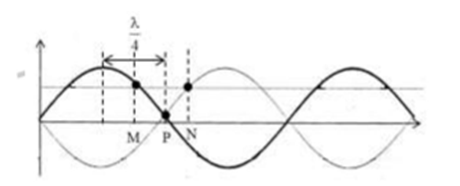
Sóng dừng trên dây với 5 nút sóng  $\large \rightarrow$ có 4 bụng sóng, chiều dài dây là: 
$\large l=k.\dfrac{\lambda}{2}\Rightarrow 1,2=4.\dfrac{\lambda}{2}\Rightarrow \lambda=0,6 (m)=60 (cm)$ 
Biên độ dao động của điểm bụng là:  $\large a_{max}=2a_0$ 
Biên độ dao động của điểm M là: 

$\large a_M=2.a_0\sin\dfrac{2\pi d}{\lambda}=\dfrac{1}{2}.2a_0\Rightarrow \sin\dfrac{2\pi d}{\lambda}=\dfrac{1}{2}$  
$\large \Rightarrow \dfrac{2\pi d}{\lambda}=\dfrac{\pi}{6}\Rightarrow d=\dfrac{\lambda}{12}=5 (cm)<\dfrac{\lambda}{8}$ 
Khoảng cách từ điểm M tới bụng gần nhất là: 
$\large d'=\dfrac{\lambda}{4}-d=\dfrac{60}{4}-5 =10 (cm)$ 
Vậy để hai điểm M, N gần nhất, chúng đối xứng nhau qua nút.
Khoảng cách giữa vị trí cân bằng của hai điểm M và N bằng: MN = 2d = 2.5 = 10 (cm)
Chọn D.