Một vật có khối lượng 400 g dao động điều hòa. Sự phụ thuộc của thế nă

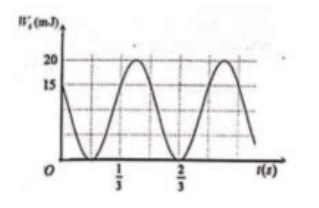
Một vật có khối lượng 400 g dao động điều hòa. Sự phụ thuộc của thế năng của vật theo thời gian được cho như hình vẽ. Tại thời điểm t = 0, vật chuyển động theo chiều dương. Lấy $\large \pi^2=10$.  Phương trình dao động của vật là

• A. A. $\large x=10.\cos\left(\pi t-\dfrac{\pi}{6}\right) (cm)$
• B. B. $\large x=5.\cos\left(2\pi t-\dfrac{\pi}{3}\right) (cm)$
• C. C. $\large x=5.\cos\left(2\pi t-\dfrac{5\pi}{6}\right) (cm)$
• D. D. $\large x=10.\cos\left(\pi t+\dfrac{\pi}{6}\right) (cm)$

Phương pháp: 
Sử dụng kĩ năng đọc đồ thị 
Thế năng của con lắc lò xo: $\large W_t=\dfrac{1}{2}kx^2$
Thế năng biến thiên với chu kì: $\large T'=\dfrac{T}{2}$  
Cơ năng: $\large W=nW_t\Rightarrow x=\pm \dfrac{A}{\sqrt{n}}$ 
Sử dụng vòng tròn lượng giác 
Cách giải:
Từ đồ thị ta thấy khoảng thời gian giữa 2 ô là: $\large \dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3} (s)$ 
Chu kì biến thiên của thế năng là 3 ô $\large \Rightarrow T'=\dfrac{3}{2}.\dfrac{1}{3}=0,5 (s)$ 
Thế năng biến thiên với chu kì: $\large T'=\dfrac{T}{2}\Rightarrow T=2T'=2.0,5=1 (s)$ 
Tại thời điểm  $\large t=0$ thế năng của vật đang giảm $\large \rightarrow$  li độ giảm.
Ta có:
$\large W_t=15 (mJ)=\dfrac{3}{4}W_{t max}=\dfrac{3}{4}W\Rightarrow W=\dfrac{4}{3}W_t\Rightarrow x=\pm \dfrac{1}{\sqrt{\dfrac{4}{3}}}A=\pm \dfrac{A\sqrt{3}}{2}$ 
Tại thời điểm $\large t=0$  vật chuyển động theo chiều dương, ta có vòng tròn lượng giác:

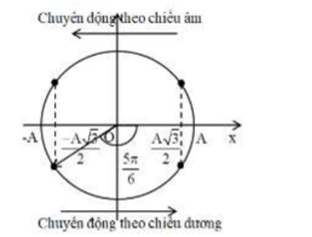
Từ vòng tròn lượng giác, ta thấy pha ban đầu của dao động là: $\large \varphi =-\dfrac{5\pi}{6} (rad)$
Thế năng cực đại của vật là:  
$\large W_{t max}=W=\dfrac{1}{2}m\omega^2A^2\Rightarrow 20.10^{-3}=\dfrac{1}{2}.0,4.(2\pi)^2.A^2\Rightarrow A=0,05 (m)=5 (cm)$ 
Phương trình dao động của vật là: $\large x=5.\cos\left(5\pi t-\dfrac{5\pi}{6} \right ) (cm)$ 
Chọn C.