Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m, vật nh

Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m, vật nhỏ khối lượng m = 100 g. Nâng vật lên theo phương thẳng đứng để lò xo nén 3 cm rồi truyền cho vật vận tốc đầu $\large 30\pi  cm/s$ hướng thẳng đứng xuống dưới. Trong một chu kì, khoảng thời gian lực đàn hồi của lò xo có độ lớn nhỏ hơn 2 N gần nhất với giá trị nào sau đây?  

• A. A. 0,02 s.
• B. B. 0,06 s.
• C. C. 0,05 s
• D. D. 0,04 s.

Phương pháp:
Tần số góc của con lắc lò xo: $\large \omega =\sqrt{\dfrac{k}{m}}$
Độ giãn của lò xo ở VTCB: $\large \Delta l_0=\dfrac{mg}{k}$
Công thức độc lập với thời gian: $\large x^2+\dfrac{v^2}{\omega^2}=A^2$ 
Độ lớn lực đàn hồi của lò xo: $\large F_{dh}=k.\Delta l$  
Sử dụng vòng tròn lượng giác và công thức: $\large \Delta t=\dfrac{\Delta \varphi}{\omega}$ 
Cách giải: 
Tần số góc của con lắc là: $\large \omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,01}}=10\sqrt{10}=10\pi (rad/s)$ 
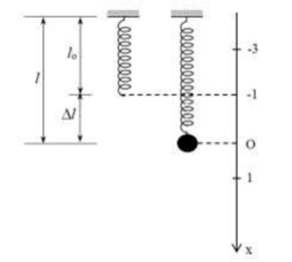
Ở VTCB, lò xo giãn một đoạn là: $\large \Delta l_0=\dfrac{mg}{k}=\dfrac{0,1.10}{100}=0,01 (m)=1 (cm)$
Nâng vật lên để lò xo nén 3 cm, li độ của con lắc khi đó là: $\large x=-(3+1)=-4 (cm)$ 
Ta có công thức độc lập với thời gian:
$\large x^2+\dfrac{v^2}{\omega^2}=A^2\Rightarrow (-4)^2+\dfrac{(30\pi)^2}{(10\pi)^2}=A^2\Rightarrow A=5 (cm)$ 
Độ lớn của lực đàn hồi là:
$\large F_{dh}=k.\Delta l\Rightarrow \Delta l=\dfrac{F_{dh}}{k}<\dfrac{2}{100}=-0,02(m)= 2(cm)\Rightarrow -3< x <1 (cm)$ 

Ta có vòng tròn lượng giác: 

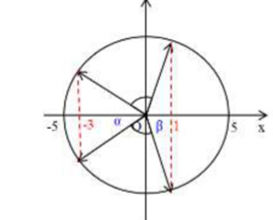
Từ vòng tròn lượng giác, ta có: $\large \left\{\begin{align}& \cos\alpha =\dfrac{3}{5}\Rightarrow \alpha \approx 53^\circ\\& \cos\beta =\dfrac{1}{5}\Rightarrow \beta \approx 78^\circ\\\end{align}\right.$
Vậy trong khoảng thời gian lực đàn hồi có độ lớn nhỏ hơn 2 N, vecto quay được góc:
$\large \Delta \varphi=2.(180-53-78)=98^\circ\approx 1,71 (rad)\Rightarrow \Delta t=\dfrac{\Delta \varphi}{\omega}=\dfrac{1,71}{10\pi}=0,054 (s)$ 
Vậy giá trị thời gian gần nhất là 0,05 s 
Chọn C.