Trên một sợi dây dài, đang có sóng ngang truyền qua. Hình dạng của một
MỤC LỤC
Câu hỏi:
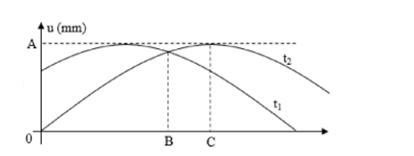
Trên một sợi dây dài, đang có sóng ngang truyền qua. Hình dạng của một đoạn dây tại hai thời điểm t1 và t2 như hình vẽ. Li độ của các phần tử tại B và C ở thời điểm t1 lần lượt là 10√3mm và 10mm. Biết Δt=t2−t1=0,056s và nhỏ hơn một chu kì sóng. Tốc độ dao động cực đại của các phần tử trên dây bằng

Đáp án án đúng là: C
Lời giải chi tiết:
Phương pháp:
+ Đọc đồ thị
+ Sử dụng vòng tròn lượng giác
Cách giải:
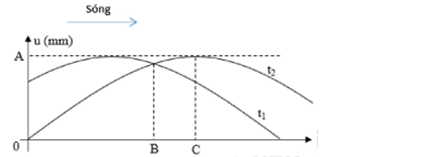
Từ đồ thị, xác định các điểm B, C tại thời điểm t1,t2 trên vòng tròn lượng giác, ta có:
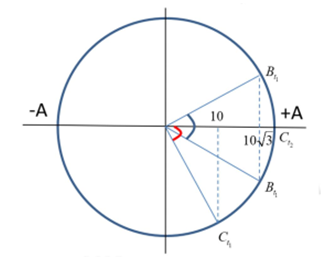
Ta có: ΔφC(t1→t2)=ΔφB(t1→t2)=α=ω.Δt
Từ vòng tròn lượng giác, ta có: {cosα=10Acosα2=10√3A
Từ đây ta suy ra: cosα=12⇒α=60∘=π3⇒A=20mm
Lại có: α=ω.Δt⇒ω=αΔt=π30,056=40π(rad/s)
Tốc độ dao động cực đại của các phần tử dao động trên dây:
vmax=Aω=20.40π=800π(mm/s)=0,8π(m/s)
Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Đặt điện áp xoay chiều có biểu thức u=200cos(ωt)(V) t
- Một vật tham gia đồng thời 3 dao động điều hòa 1, 2, 3 cùng phương cùn
- Một con lắc lò xo có độ cứng 50 N/m đang dao động điều hòa với biên độ
- Trên một sợi dây có sóng dừng, hai điểm A và B là hai điểm bụng gần nh
- Đặt điện áp xoay chiều u=U0cos(ωt) (V) (U0