Đặt điện áp xoay chiều $\large u=U_0\cos (\omega t)$ (V) ($\large U_0$

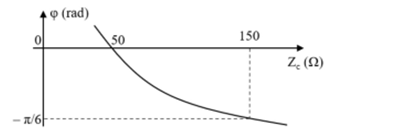
Đặt điện áp xoay chiều $\large u=U_0\cos (\omega t)$ (V) ($\large U_0$ và $\large \omega$ không đổi) vào hai đầu một đoạn mạch mắc nối tiếp gồm điện trở R, cuộn cảm thuần có hệ số tự cảm L và tụ điện có điện dung C thay đổi được. Gọi   là cường độ dòng điện tức thời qua mạch,  $\large \varphi$ là độ lệch pha giữa u và i. Đồ thị biểu diễn sự phụ thuộc của $\large \varphi$  theo dung kháng  $\large Z_C$ của tụ điện khi C thay đổi như hình vẽ. Khi  $\large Z_C=100\Omega$ thì  $\large \varphi$ nhận giá trị 

• A. A. -0,17 rad
• B. B. -0,22 rad
• C. C. -0,28 rad
• D. D. -0,26 rad

Phương pháp: 
+ Đọc đồ thị 
+ Sử dụng biểu thức: $\large \tan\varphi=\dfrac{Z_L-Z_C}{R}$
Cách giải: 
Từ đồ thị, ta có: 
+ Khi  $\large Z_C=50\Omega$ thì $\large \varphi=0$ Xảy ra cộng hưởng điện $\large \Rightarrow Z_C=Z_L=50\Omega$  
+ Khi $\large Z_C=150\Omega$ thì $\large \varphi =-\dfrac{\pi}{6}$  
Ta có:  $\large \tan\varphi=\dfrac{Z_L-Z_C}{R}\Leftrightarrow \tan\left ( -\dfrac{\pi}{6} \right )=\dfrac{50-150}{R}\Rightarrow R=100\sqrt{3}\Omega$
+ Khi $\large Z_C=100\Omega$ thì $\large \tan\varphi=\dfrac{Z_L-Z_C}{R}=\dfrac{50-100}{100\sqrt{3}}=-\dfrac{\sqrt{3}}{6}\Rightarrow \varphi=-0,281 (rad)$
Chọn C.