Cho đoạn mạch gồm 3 phần tử R, L, C mắc nối tiếp, trong đó cuộn dây th

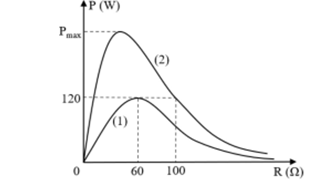
Cho đoạn mạch gồm 3 phần tử R, L, C mắc nối tiếp, trong đó cuộn dây thuần cảm và điện trở R biến thiên. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức  $\large u=U_0\cos (2\pi ft)$, $\large U_0$ không đổi nhưng, $\large f$ có thể thay đổi được. Cho đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ điện của mạch theo R như hình vẽ: Khi  $\large f=f_1$ là đường (1), khi  $\large f=f_2$ là đường (2). Giá trị của  $\large P_{max}$ bằng 

• A. A. 173W
• B. A. 173W
• C. C. 137W
• D. D. 161W

Phương pháp: 
+ Đọc đồ thị P-t 
+ Sử dụng biểu thức tính công suất: $\large P=\dfrac{U^2}{R^2+(Z_L-Z_C)^2}.R$
Cách giải: 
Ta có:  
+ Khi $\large f=f_1:P_{1max}=120W=\dfrac{U^2}{2R_1}$ với $\large R_1=60\Omega$ ta suy ra: ​​​​​​​$\large U = 120V$ 
+ Khi ​​​​​​​$\large f=f_2$:  
Tại vị trí ​​​​​​​$\large R_2=100\Omega$ có ​​​​​​​$\large P=120W$  
Ta có: ​​​​​​​$\large  P=\dfrac{U^2}{R^2_2+(Z_L-Z_C)^2}.R_2\Leftrightarrow 120=\dfrac{120^2}{100^2+(Z_L-Z_C)^2}.100\Rightarrow |Z_L-Z_C|=20\sqrt{5}\Omega$
Lại có: ​​​​​​​$\large P_{2max}=\dfrac{U^2}{2R'}=\dfrac{U^2}{2|Z_L-Z_C|}=\dfrac{120^2}{2.20\sqrt{5}}=72\sqrt{5}W$ 
Chọn D.