Một vật có khối lượng 100 g dao động điều hòa với tần số 5 Hz và biên

Một vật có khối lượng 100 g dao động điều hòa với tần số 5 Hz và biên độ 8 cm. Lấy $\large \pi^2=10$. Trong khoảng thời gian ngắn nhất giữa hai lần lực kéo về có độ lớn $\large 4\sqrt{3}N$ thì vật có tốc độ trung bình là 

• A.

  A. $\large 1,2m/s$

• B.

  B. $\large 2,4m/s$

• C.

  C. $\large 2,4\sqrt{3} m/s$

• D.

  D. $\large 0,643 m/s$

Phương pháp: 
+ Sử dụng biểu thức tính chu kì: $\large T=\dfrac{1}{f}$
+ Vận dụng biểu thức: $\large \omega =\sqrt{\dfrac{k}{m}}$
+ Sử dụng biểu thức lực kéo về: $\large F_{kv}=-kx$  
+ Tốc độ trung bình: $\large v_{tb}=\dfrac{S}{t}$ 
Cách giải: 
Ta có: 
+ Chu kì dao động của vật: $\large T=\dfrac{1}{f}=\dfrac{1}{5}=0,2s$ 
+ Tần số góc: $\large \omega =10\pi (rad/s)$ 
Lại có : $\large \omega =\sqrt{\dfrac{k}{m}}\Rightarrow k=m.\omega^2=0,1.(10\pi)^2=100 N/m$
+ Tại vị trí lực kéo về có độ lớn $\large 4\sqrt{3}N: |F_{kv}|=4\sqrt{3}\Rightarrow |kx|=4\sqrt{3}\Rightarrow x=\pm 0,04\sqrt{3} m=\pm 4\sqrt{3} cm$ 

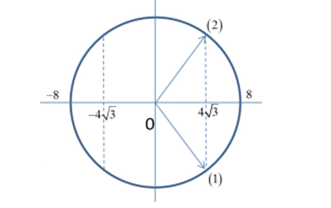
+ Thời gian ngắn nhất giữa hai lần lực kéo về có độ lớn  $\large 4\sqrt{3}N$ là $\large t=2\dfrac{T}{12}=\dfrac{T}{6}=\dfrac{1}{30}s$  
+ Quãng đường vật đi được trong khoảng thời gian đó là: $\large S=2(8-4\sqrt{3})=16-8\sqrt{3} cm$
Tốc độ trung bình của vật khi đó: $\large v_{tb}=\dfrac{S}{t}=\dfrac{16-8\sqrt{3}}{\dfrac{1}{30}}=64,3 cm/s=0,643 m/s$
Chọn D.