Tìm m để phương trình $\large 3 \sqrt{\tan x+1}(\sin x+2 \cos x)=m(\si

Tìm m để phương trình

$\large 3 \sqrt{\tan x+1}(\sin x+2 \cos x)=m(\sin x+3 \cos x)(1)$

có nghiệm duy nhất thuộc khoảng $\large \left(0 ; \dfrac{\pi}{2}\right)$.

• A. A. Không tồn tại m thỏa mãn.
• B. B. $\Large m>2$
• C. C. $\Large m\geq2$
• D. D. $\Large m=2$

Xét $\large x \in\left(0 ; \dfrac{\pi}{2}\right)$, khi đó sin x>0.

$\large \cos x>0, \tan x>0$ và $\large \sin x+3 \cos x>0$.

PT (1) $\large \Leftrightarrow 3 \sqrt{\tan x+1} \cdot\left(\dfrac{\sin x+2 \cos x}{\sin x+3 \cos x}\right)=m$

$\large \Leftrightarrow 3 \sqrt{\tan x+1} \cdot\left(\dfrac{\tan x+2}{\tan x+3}\right)=m$ (2)

Đặt $\large t=\tan t, t>0$, PT (2) thành

$\large 3 \sqrt{t+1} \cdot \dfrac{t+2}{t+3}=m$ (3)

Xét hàm số $\large f(t)=3 \sqrt{t+1} \cdot \dfrac{t+2}{t+3},(t>0)$.

$\large f^{\prime}(t)=\dfrac{3}{2 \sqrt{t+1}} \cdot \dfrac{t+2}{t+3}+\dfrac{3 \sqrt{t+1}}{(t+3)^{2}}>0 ; \forall t>0$

Ta có bảng biến thiên

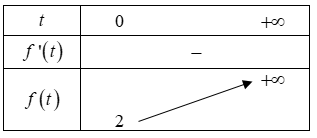
Ứng với mỗi t>0 thỏa mãn PT (3), ta được đúng một nghiệm $\large x \in\left(0 ; \dfrac{\pi}{2}\right)$ của PT (1). Do đó PT (1) có nghiệm duy nhất $\large x \in\left(0 ; \dfrac{\pi}{2}\right)$ khi và chỉ khi PT (3) có duy nhất nghiệm t>0. Căn cứ vào bảng biến thiên ta suy ra m>2.