Tìm tất cả các giá trị thực của tham số $m$ để phương trình $\Large 2

Tìm tất cả các giá trị thực của tham số $m$ để phương trình $\Large 2 x^{3}-3 x^{2}+2-2^{1-2 m}=0$ có 3 nghiệm thực phân biệt

• A.

  A. $\Large \dfrac{1}{2} < m < 1$

• B.

  B. $\Large 0 < m < \dfrac{1}{2}$

• C.

  C. $\Large -1 < m < \dfrac{1}{2}$

• D.

  D. $\Large -1 < m < 0$

$\Large 2 x^{3}-3 x^{2}+2-2^{1-2 m}=0 \Leftrightarrow 2 x^{3}-3 x^{2}+2=2^{1-2 m}$

Xét hàm số $\Large f(x)=2 x^{3}-3 x^{2}+2$

TXĐ: $\Large D=\mathbb{R}$. Có $\Large y^{\prime}=6 x^{2}-6 x=0 \Leftrightarrow\left[\begin{array}{l}
x=0 \\
x=1
\end{array}\right.$

Lập BBT:

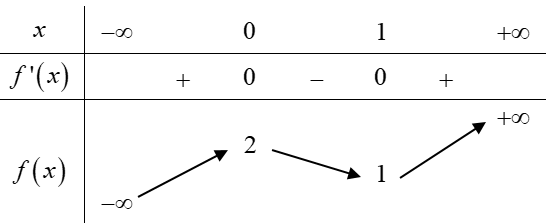
Số nghiệm của phương trình $2 x^{3}-3 x^{2}+2=2^{1-2 m}$ là số giao điểm của đồ thị hàm số $f(x)=2 x^{3}-3 x^{2}+2$ và đường thẳng $y=2^{1-2 m}$

Dựa vào BBT, phương trình có 3 nghiệm phân biệt

$\Rightarrow 1 < 2^{1-2 m} < 2 \Leftrightarrow 0 < 1-2 m < 1 \Leftrightarrow 0 < m < \dfrac{1}{2}$

Chọn B