Cho ba hàm số $\large y=f(x), y=g(x), y=h(x)$ có đồ thị của các hàm số

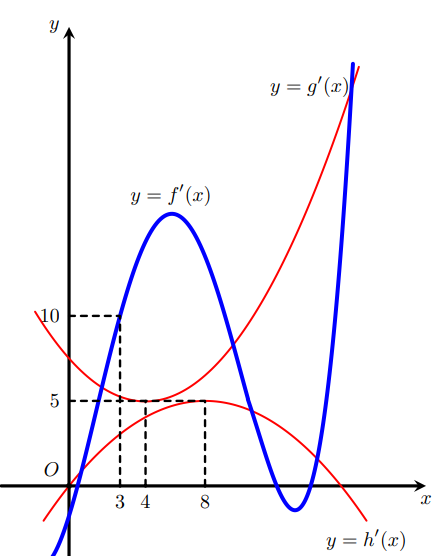
Cho ba hàm số $\large y=f(x), y=g(x), y=h(x)$ có đồ thị của các hàm số $\large y=f^{\prime}(x), y=g^{\prime}(x)$ và $\large y=h^{\prime}(x)$ như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số $\large y=f^{\prime}(x)$. Hàm số $\large k(x)=f(x+7)+g\left(2 x+\dfrac{15}{2}\right)-h\left(4 x+\dfrac{3}{2}\right)$ đồng biến trên khoảng nào dưới đây?

• A.

  A. $\large \left(-\dfrac{17}{4} ; 0\right)$.

• B.

  B. $\large \left(-\infty ; \dfrac{1}{4}\right)$.

• C.

  C. $\large \left(\dfrac{3}{8} ; 1\right)$.

• D.

  D. $\large \left(\dfrac{3}{8} ;+\infty\right)$.

Chọn C

Ta có: $\Large k'(x)=f'(x+7) + 2g'\left(2x+\dfrac{15}{2}\right)-4h'\left(4x+\dfrac{3}{2}\right)$

Xét đáp án C

* $\Large \dfrac{3}{8} 10$

* $\Large $ $\Large \dfrac{3}{8}< x<1\Leftrightarrow 8,25 <2x+\dfrac{15}{2}<9,5\Rightarrow g'\left(2x+\dfrac{15}{2}\right) >5\Rightarrow 2g'\left(2x+\dfrac{15}{2}\right) >10$

* $\Large \dfrac{3}{8} < x<1\Leftrightarrow 3<4x+\dfrac{3}{2} <5,5\Rightarrow h'\left( 4x+\dfrac{3}{2}\right) <20$ 

Suy ra: $\Large k'(x)= f'(x+7) + 2g'\left( 2x+\dfrac{15}{2}\right) -4h'\left( 4x+\dfrac{3}{2}\right) >10+ 10-20=0$

Vậy hàm số $\Large k(x)$ đồng biến trên $\Large \left(\dfrac{3}{8}; 1\right)$