Cho hàm số đa thức bậc bốn $y=f\left( x \right)$ có đồ thị là đường co

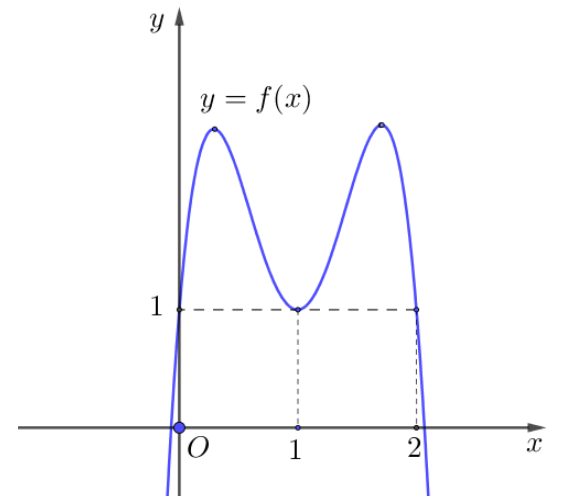
Cho hàm số đa thức bậc bốn $y=f\left( x \right)$ có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình $f\left( \frac{4f\left( x \right)}{\ln {{x}^{2}}} \right)-1=0$ là:

• A. A. 8
• B. B. 5
• C. C. 6
• D. D. 4

$f\left( \frac{4f\left( x \right)}{\ln {{x}^{2}}} \right)-1=0\Leftrightarrow \left[ \begin{matrix}   & \frac{4f\left( x \right)}{\ln {{x}^{2}}}=0 \\   & \frac{4f\left( x \right)}{\ln {{x}^{2}}}=1 \\   & \frac{4f\left( x \right)}{\ln {{x}^{2}}}=2 \\  \end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}   & f\left( x \right)=0\left( 1 \right) \\   & f\left( x \right)=\frac{1}{2}\ln \left| x \right|\left( 2 \right) \\   & f\left( x \right)=\ln \left| x \right|\left( 3 \right) \\  \end{matrix} \right.$
$f\left( x \right)=0\Leftrightarrow \left[ \begin{matrix}   & x={{x}_{1}}<0 \\   & x={{x}_{2}}>2 \\  \end{matrix} \right.$
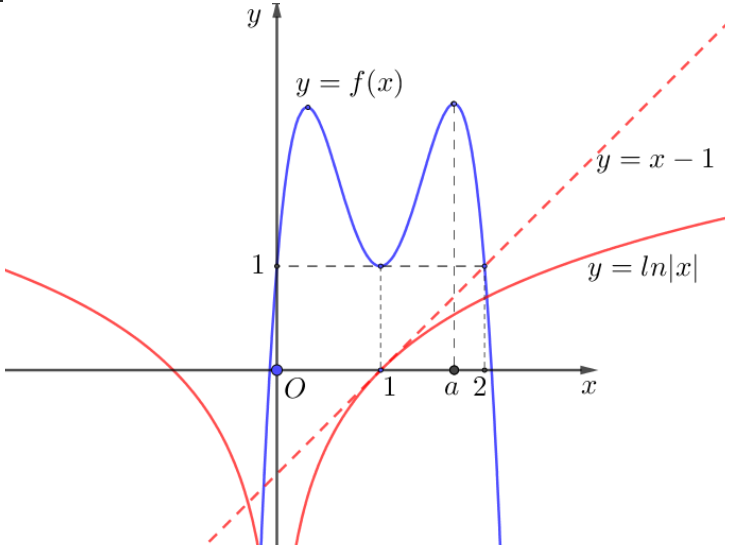
Xét phương trình $f\left( x \right)=\ln \left| x \right|$, vì $y=f\left( x \right)$ là hàm số đa thức bậc bốn nên ta có:
+) Trên $\left( -\infty ;0 \right)$ đồ thị hàm số $y=\ln \left| x \right|$ cắt đồ thị hàm số $y=f\left( x \right)$ tại duy nhất một điểm.
+) Trên $\left( 0;a \right)$, với $x=a\in \left( 1;2 \right)$ là một điểm cực đại của hàm số $y=f\left( x \right)$$\ln \left| x \right|=\ln x\le x-1 +) Trên $\left( a;+\infty  \right)$, ta thấy đồ thị hàm số $y=\ln x$ cắt đồ thị hàm số $y=f\left( x \right)$ tại duy nhất một điểm.
Do đó, phương trình $f\left( x \right)=\ln \left| x \right|$ có đúng 2 nghiệm phân biệt và hai nghiệm này khác với hai nghiệm của phương trình (1)
Xét phương trình  $\Large f(x)=\dfrac{1}{2}ln|x|$. Tương tự như phương trình (2) và với đánh giá   $\Large \dfrac{1}{2}ln|x|=\dfrac{1}{2}(x-1)

Vậy phương trình đã cho có 6 nghiệm phân biệt