Cho hàm số y = f(x) có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số

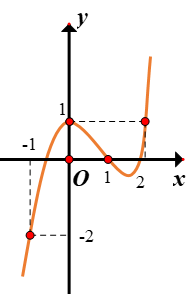
Cho hàm số y = f(x) có đạo hàm trên $\large \mathbb{R}$. Đồ thị hàm số y=f'(x) như hình vẽ bên dưới

Hàm số $\large g(x)=f(x)-\dfrac{x^{3}}{3}+x^{2}-x+2$ đồng biến trên khoảng nào trong các khoảng sau?

• A.

  A. (-1;0)

• B.

  B. (0;2)

• C.

  C. (1;2)

• D.

  D. (0;1)

Chọn D

Ta có $\large g^{\prime}(x)=f^{\prime}(x)-x^{2}+2 x-1, g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=(x-1)^{2}$.

Suy ra số nghiệm của phương trình $\large g^{\prime}(x)=0$ chính là số giao điểm giữa đồ thị hàm số (C) $\large y=f^{\prime}(x)$ và parabol $\large (P): y=(x-1)^{2}$

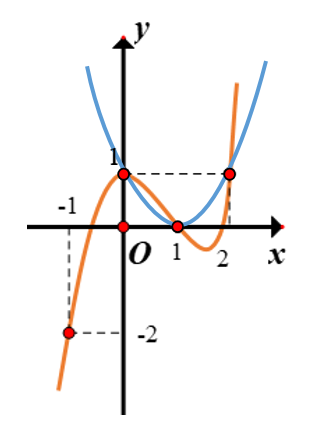
Dựa vào đồ thị ta suy ra $\large g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=0 \\
x=1 \\
x=2
\end{array}\right.$.

Bảng biến thiên

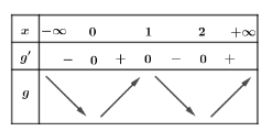
Dựa vào bảng biến thiên suy ra g(x) đồng biến trên $\Large (0;1)\cup(2;+\infty)$.

Suy ra đáp án đúng: D