Tìm m để bất phương trình $\large m\left(\sqrt{x^{2}-2 x+2}+1\right)+x

Tìm m để bất phương trình

$\large m\left(\sqrt{x^{2}-2 x+2}+1\right)+x(2-x) \leq 0\quad(1)$

có nghiệm kép $\large x \in[0 ; 1+\sqrt{3}]$.

• A.

  $\Large m\leq\dfrac{2}{3}$

• B.

  $\Large m>\dfrac{2}{3}$

• C.

  $\Large m=0$

• D.

  Không tồn tại m thỏa mãn

Đặt $\large t=\sqrt{x^{2}-2 x+2}$.

Ta có $\large t^{\prime}=\dfrac{2 x-2}{2 \sqrt{x^{2}-2 x+2}} ; t^{\prime}=0 \Leftrightarrow x=1$. Ta có bảng biến thiên

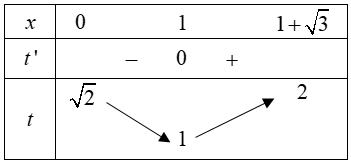
Từ đó $\large 1 \leq t \leq 2$. Với $\large 1 \leq t \leq 2$, ta biến đổi

$\large t=\sqrt{x^{2}-2 x+2} \Leftrightarrow t^{2}=x^{2}-2 x+2$ $\large \Leftrightarrow t^{2}-2=-x(2-x)$.

BPT (1) trở thành: $\large m(t+1) \leq t^{2}-2 \Leftrightarrow m \leq \dfrac{t^{2}-2}{t+1}\quad(2)$

Xét hàm số $\large f(t)=\dfrac{t^{2}-2}{t+1},(1 \leq t \leq 2)$, có: $\large f^{\prime}(t)=\dfrac{t^{2}+2 t+2}{(t+1)^{2}}>0 \quad, \forall t \in[1 ; 2]$

Suy ra hàm số f(t) đồng biến trên [1;2].

Bảng biến thiên

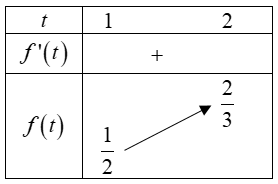
Từ bảng biến thiên, BPT (1) có nghiệm $\large x \in[0 ; 1+\sqrt{3}]$ khi và chỉ khi BPT (2) có nghiệm $\large t \in[1 ; 2]$.

Điều này xảy ra khi $\large m \leq \max _{t \in|1;2|} f(t)=f(2)=\dfrac{2}{3}$.