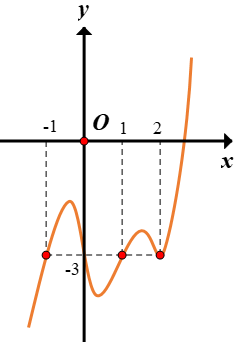
Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$ và đồ thị hình b
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x) có đạo hàm trên $\large \mathbb{R}$ và đồ thị hình bên dưới là đồ thị của đạo hàm f'(x). Hỏi hàm số g(x)=f(x)+3 x có bao nhiêu điểm cực trị?
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
Ta có $\large g^{\prime}(x)=f^{\prime}(x)+3 ; g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=-3$. Suy ra số nghiệm của phương trình $\large g^{\prime}(x)=0$ chính là số giao điểm giữa đồ thị của hàm số $\large f^{\prime}(x)$ và đường thẳng y=-3.
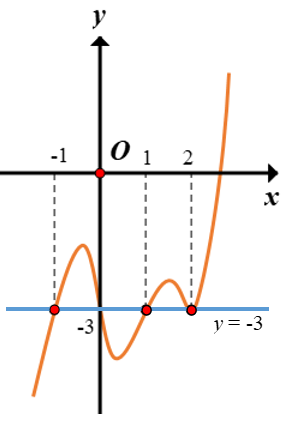
Dựa vào đồ thị ta suy ra $\large g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=-1 \\
x=0 \\
x=1 \\
x=2
\end{array}\right.$. Ta thấy x=-1, x=0, x=1 là các nghiệm đơn và x=2 là nghiệm kép nên đồ thị hàm số $\large g(x)=f(x)+3 x$ có 3 điểm cực trị. Chọn B.
Xem thêm các bài tiếp theo bên dưới
- Một người có một dây ruy bằng dài 130cm, người đó cần bọc dải ruy băng
- Cho hàm số $\large y=x^{3}+(1-2 m) x^{2}+(2-m) x+m+2(1)$. Tìm tập hợp
- Tìm tất cả giá trị của tham số m để hàm số $\large y=m x^{4}+\left(m^{
- Cho hàm số y=f(x) có đạo hàm liên tục trên $\large \mathbb{R}$. Đồ thị
- Cho hàm số f(x) có đạo hàm trên $\large \mathbb{R}$ và đồ thị hàm $\la