Cho hàm số y=f(x) có đạo hàm liên tục trên $\large \mathbb{R}$. Đồ thị

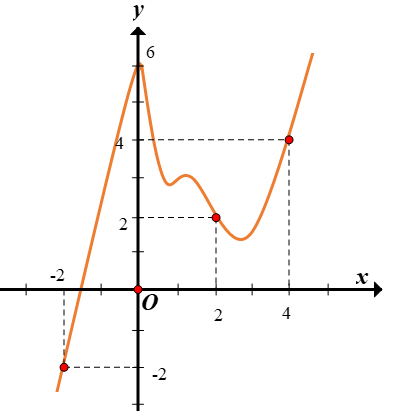
Cho hàm số y=f(x) có đạo hàm liên tục trên $\large \mathbb{R}$. Đồ thị hàm số $\large y=f^{\prime}(x)$ như hình bên dưới.

Hàm số $\large g(x)=2 f(x)-x^{2}$ đồng biến trên khoảng nào trong các khoảng sau đây?

 

• A.

  A. $\large (-\infty ;-2)$

• B.

  B. (-2;2)

• C.

  C. (2;4)

• D.

  D. $\large (2 ;+\infty)$

Chọn B

 Ta có $\large g^{\prime}(x)=2 f^{\prime}(x)-2 x \Rightarrow g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=x$

Số nghiệm của phương trình $\large g^{\prime}(x)=0$ chính là số giao điểm của đồ thị hàm số $\large y=f^{\prime}(x)$ và đường thẳng d: y=x (như hình vẽ bên dưới).

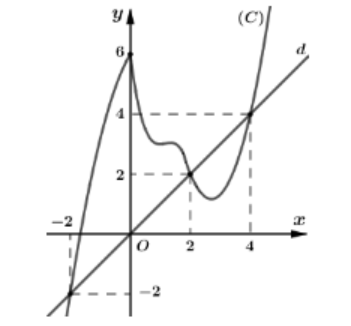
Dựa vào đồ thị, suy ra $\large g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=-2 \\
x=2 \\
x=4
\end{array}\right.$.

Lập bảng biến thiên

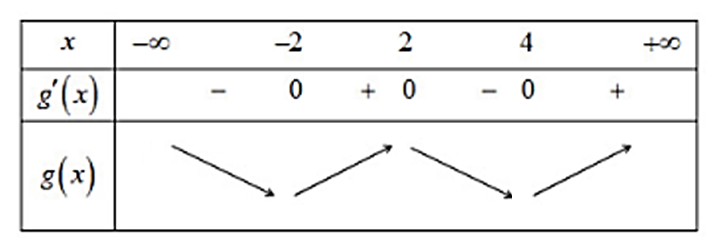
$\large \Rightarrow$ hàm số g(x) đồng biến trên $\large (-2 ; 2) \text { và }(4 ;+\infty)$. So sánh 4 đáp án. Chọn B.