Cho x, y, z dương thỏa mãn $\large 2 x+4 y+7 z=2 x y z$. Tìm GTNN của

Cho x, y, z dương thỏa mãn $\large 2 x+4 y+7 z=2 x y z$. Tìm GTNN của $\Large P=x+y+z$

• A.

  $\Large m=\dfrac{15}{2}$

• B.

  $\Large m=\dfrac{2}{7}$

• C.

  $\Large m=\dfrac{4}{9}$

• D.

  $\Large m=\dfrac{13}{4}$

Từ $\large 2 x+4 y+7 z=2 x y z \Leftrightarrow z(2 x y-7)=2 x+4 y \Rightarrow 2 x y-7>0$ và $\large z=\dfrac{2 x+4 y}{2 x y-7}$

$\large \Rightarrow P=x+y+z=x+y+\dfrac{2 x+4 y}{2 x y-7}=x+\dfrac{2 x y-7+7}{2 x}+\dfrac{2 x^{2}+(4 x y-14)+14}{x(2 x y-7)}$

$\large =x+\dfrac{2 x y-7}{2 x}+\dfrac{7}{2 x}+\dfrac{2 x^{2}+14}{x(2 x y-7)}+\dfrac{2}{x}=x+\dfrac{11}{2 x}+\left(\dfrac{2 x y-7}{2 x}\right)+\dfrac{2 x^{2}+14}{x(2 x y-7)}$

Do $\large \left(\dfrac{2 x y-7}{2 x}\right)+\dfrac{2 x^{2}+14}{x(2 x y-7)} \geq 2 \sqrt{\dfrac{x^{2}+7}{x^{2}}} \Rightarrow P \geq x+\dfrac{11}{2 x}+2 \sqrt{\dfrac{x^{2}+7}{x^{2}}}$

Xét hàm số $\large f(x)=x+\dfrac{11}{2 x}+2 \sqrt{\dfrac{x^{2}+7}{x^{2}}} \quad(x>0)$.

Ta có $\large f^{\prime}(x)=1-\dfrac{11}{2 x^{2}}-\dfrac{14}{x^{2} \sqrt{x^{2}+7}}$;

Ta có: $\large f^{\prime}(x)=0$ đặt $\large t=\sqrt{x^{2}+7} (t>0)$ ta được $\large 2 t^{3}-25 t-28=0 \Rightarrow t=4 \Leftrightarrow x=3$

Lập BBT của f(x)

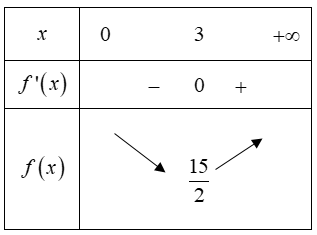
$\large \Rightarrow P \geq \dfrac{15}{2}$. Đẳng thức xảy ra khi $\large x=3; y=\dfrac{5}{2} ; z=2$

Vậy giá trị nhỏ nhất của P là $\large \dfrac{15}{2}$