Bạn Hoa đi từ nhà ở vị trí A đến trường học tại vị trí C phải đi qua c

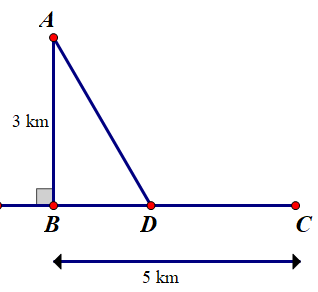
Bạn Hoa đi từ nhà ở vị trí A đến trường học tại vị trí C phải đi qua cầu từ vị trí A đến B rồi từ B đến trường. Trận lũ lụt vừa qua cây cầu bị ngập nước, do đó bạn Hoa phải đi bằng thuyền từ nhà đến một vị trí D nào đó ở trên đoạn BC với vận tốc 4km/h sau đó đi bộ với vận tốc 5km/h đến C. Biết AB=3km, BC=5km. Hỏi muộn nhất mấy giờ bạn Hoa phải xuất phát từ nhà để có mặt ở trường lúc 7 giờ 30 phút sáng kịp vào học?

• A.

  A. 6h03 phút

• B.

  B. 6h16 phút

• C.

  C. 5h30 phút

• D.

  D. 5h34 phút

Gọi BD=x (km); DC=y (km). Khi đó: BC = BD + DC = x + y= 5

Xét tam giác ABD vuông tại B có $\large \mathrm{AD}=\sqrt{\mathrm{AB}^{2}+\mathrm{BD}^{2}}=\sqrt{\mathrm{x}^{2}+9}$

Thời gian bạn hoa đi từ A đến D là: $\large t_{A D}=\dfrac{\sqrt{x^{2}+9}}{4} h$.

Thời gian bạn Hoa đi từ D đến C là: $\large t_{\mathrm{DC}}=\dfrac{y}{5} h$.

Khi đó tổng thời gian bạn Hoa đi từ nhà đến trường là:

$\large \mathrm{T}=\dfrac{\sqrt{\mathrm{x}^{2}+9}}{4}+\dfrac{\mathrm{y}}{5} \Rightarrow f(x)=\dfrac{\sqrt{\mathrm{x}^{2}+9}}{4}+\dfrac{5-\mathrm{x}}{5}$

Xét hàm số $\large f(x)=\dfrac{\sqrt{x^{2}+9}}{4}+\dfrac{5-x}{5}, f^{\prime}(x)=\dfrac{x}{4 \sqrt{x^{2}+9}}-\dfrac{1}{5} ; f^{\prime}(x)=0$ $\large \Leftrightarrow 5 x=4 \sqrt{x^{2}+9} \Leftrightarrow x=4$

Dựa vào bảng biến thiên, ta được $\large \min f(x)=f(4)=\dfrac{29}{20}=87$ phút.

Do đó bạn Hoa phải xuất phát muộn nhất từ nhà lúc 6h03 phút để có mặt ở trường lúc 7h30 phút. Chọn A.