Thiết diện qua trục hình nón là một tam giác vuông cân có cạnh góc vuô

Thiết diện qua trục hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích toàn phần và thể tích hình nón có giá trị lần lượt là:

• A.

  A. $\large \dfrac{(1+\sqrt{2})\pi a^{2}}{2}$ và $\large \dfrac{\sqrt{2}\pi a^{3}}{12}$

• B.

  B. $\large \dfrac{\sqrt{2}\pi a^{2}}{2}$ và $\large \dfrac{\sqrt{2}\pi a^{3}}{4}$

• C.

  C. $\large \dfrac{(1+\sqrt{2})\pi a^{2}}{2}$ và $\large \dfrac{\sqrt{2}\pi a^{3}}{4}$

• D.

  D. $\large \dfrac{\sqrt{2}\pi a^{2}}{2}$ và $\large \dfrac{\sqrt{2}\pi a^{3}}{12}$

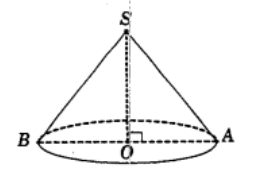
Gọi S, O là đỉnh và tâm đường tròn đáy của hình nón, thiết diện qua đỉnh là tam giác SAB.

Theo bài ra ta có tam giác SAB vuông cân tại S nên $\large AB = SB\sqrt{2} = a\sqrt{2}$, 

$\large SO = \dfrac{SB\sqrt{2}}{2} = \dfrac{a\sqrt{2}}{2}$ 

Suy ra h = SO = $\large \dfrac{a\sqrt{2}}{2}$, l = SA = a và 

$\large SB\sqrt{2} = 2R\Rightarrow R = \dfrac{SB\sqrt{2}}{2} = \dfrac{\sqrt{2}a}{2}$ 

Diện tích toàn phần của hình nón: $\large S_{tp} = \pi Rl+ \pi R^{2} = \dfrac{(1+\sqrt{2})\pi a^{2}}{2}$ (đvdt)

Thể tích khối nón là: $\large V = \dfrac{1}{3}\pi R^{2}h = \dfrac{\sqrt{2}\pi a^{3}}{12}$ (đvtt). Chọn A.