Một hình nón có bán kính đáy R , góc ở đỉnh là $\large 60^{\circ}$ . M

Một hình nón có bán kính đáy R, góc ở đỉnh là $\large 60^{\circ}$ . Một thiết diện qua đỉnh nón chắn trên đáy một cung có số đo $\large 90^{\circ}$. Diện tích của thiết diện là:

• A.

  A. $\large \dfrac{R^{2}\sqrt{7}}{2}$

• B.

  B. $\large \dfrac{R^{2}\sqrt{3}}{2}$

• C.

  C. $\large \dfrac{3R^{2}}{2}$

• D.

  D. $\large \dfrac{R^{2}\sqrt{6}}{2}$

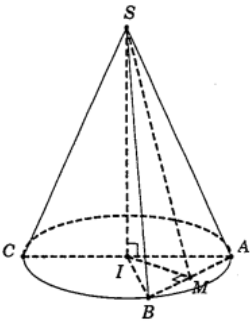
Vì góc ở đỉnh là $\large 60^{\circ}$ nên thiết diện qua trục SAC là tam giác đều cạnh 2R.

Suy ra đường cao của hình nón là $\large SI = R\sqrt{3}$.

Tam giác SAB là thiết diện qua đỉnh, chắn trên đáy cung AB có số đo bằng $\large 90^{\circ}$ nên IAB là tam giác vuông cân tại I, suy ra $\large AB = R\sqrt{2}$.

Gọi M là trung điểm của AB thì

$\large \begin{cases}
 & \ IM \perp AB \\ 
 & \ SM \perp AB 
\end{cases}$ và $\large IM = \dfrac{R\sqrt{2}}{2}$.

Trong tam giác vuông SIM, ta có:

$\large SM = \sqrt{SI^{2}+IM^{2}} = \dfrac{R\sqrt{14}}{2}$ 

Vậy $\large S_{\Delta SAB} = \dfrac{1}{2}AB.SM = \dfrac{R^{2}\sqrt{7}}{2}$ (đvdt).

Chọn A.