Một hình trụ có bán kính đáy bằng $\large \sqrt{3}$, chiều cao bằng $\

Một hình trụ có bán kính đáy bằng $\large \sqrt{3}$, chiều cao bằng $\large 2\sqrt{3}$ và gọi (S) là mặt cầu đi qua hai đường tròn đáy của hình trụ. Tính diện tích mặt cầu (S).

• A. A. $\large 6\sqrt{3}\pi$
• B. B. $\large 8\sqrt{6}\pi$
• C. C. $\large \sqrt{6}\pi$
• D. D. $\large 24\pi$

Chọn D.

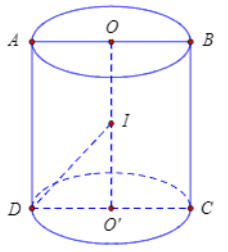
Mặt cầu (S) đi qua hai đường tròn đáy của hình trụ nên khối trụ nội tiếp khối cầu.

Mặt cầu (S) có tâm I là trung điểm của OO' và bán kính R = IA = IB = IC = ID.

Ta có $\large ID = \sqrt{O'I^{2}+O'D^{2}} = \sqrt{\left (\dfrac{2\sqrt{3}}{2}  \right )^{2}+(\sqrt{3})^{2}} = \sqrt{6} \Rightarrow S = 4\pi R^{2} = 24\pi$.