Cho hình nón đỉnh S , đường cao SO . Gọi A và B là hai điểm thuộc đườn

Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và $\large \widehat{SAO} =30^{\circ}$, $\large \widehat{SAB} =60^{\circ}$ . Diện tích xung quanh của hình nón là:

• A.

  A. $\large \pi a^{2}$

• B.

  B. $\large 3\pi a^{2}$

• C.

  C. $\large 3\pi a^{2}\sqrt{3}$

• D.

  D. $\large \pi a^{2}\sqrt{3}$

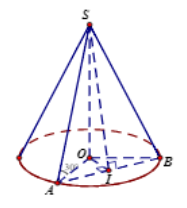
Gọi I là trung điểm của AB, ta có OI $\large \perp$ AB, SI $\large \perp$ AB, OI = a,

$\large AO = SA.cos\widehat{SAO} = SA.cos 30^{\circ} = \dfrac{\sqrt{3}}{2}SA$ 

và $\large AI = SA.cos \widehat{SAI} = SA.cos 60^{\circ} = \dfrac{1}{2}SA$ 

$\large \dfrac{AI}{AO} = \dfrac{1}{\sqrt{3}}$ 

Mà $\large \dfrac{AI}{AO} = cos \widehat{IAO} \Rightarrow cos \widehat{IAO} = \dfrac{1}{\sqrt{3}}\Rightarrow sin \widehat{IAO} = \dfrac{\sqrt{6}}{3} = \dfrac{OI}{OA} = \dfrac{a}{OA}$. 

Vậy $\large OA = \dfrac{3a}{\sqrt{6}} = \dfrac{a\sqrt{6}}{2}$ 

Xét tam giác vuông SAO, ta có: $\large SA = \dfrac{OA}{cos 30^{\circ}} = \dfrac{a\sqrt{6}}{2}.\dfrac{2}{\sqrt{3}} = a\sqrt{2}$ 

Vậy diện tích xung quanh của hình nón đã cho là: 

$\large S_{xq} = \pi .OA.SA = \pi .\dfrac{a\sqrt{6}}{2}.a\sqrt{2} = \pi a^{2}\sqrt{3}$ 

Vậy chọn đáp án D.