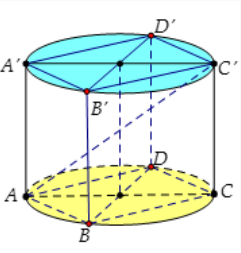
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = 8, CD = 6, AC' = 12. Tính

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = 8, CD = 6, AC' = 12. Tính diện tích toàn phần $\large S_{tp}$ của hình trụ có hai đường tròn ngoại tiếp hai hình chữ nhật ABCD và A'B'C'D'.

• A.

  A. $\large S_{tp} = 570\pi$

• B.

  B. $\large S_{tp} = 10(2\sqrt{11}+5)\pi$

• C.

  C. $\large S_{tp} = 26\pi$

• D.

  D. $\large S_{tp} = 5(4\sqrt{11}+5)\pi$

Ta có $\large 2R = AC = \sqrt{AD^{2}+CD^{2}} = \sqrt{8^{2}+6^{2}} = 10$. Suy ra:

$\large \begin{cases}
 & \ R = 5 \\ 
 & \ h = CC' = \sqrt{AC'^{2}-AC^{2}} = \sqrt{12^{2}-10^{2}} = 2\sqrt{11}
\end{cases}$ 

Khi đó diện tích toàn phần của trụ là:

$\large S_{tp} = 2\pi R(h+R) = 2\pi .5.(2\sqrt{11}+5) = 10(2\sqrt{11}+5)\pi$