Cho hình nón ( N ) có đường sinh tạo với đáy một góc $\large 60^{\circ

Cho hình nón (N) có đường sinh tạo với đáy một góc $\large 60^{\circ}$ . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N) .

• A.

  A. V = $\large 9\sqrt{3}\pi$

• B.

  B. V = $\large 9\pi$

• C.

  C. V = $\large 3\sqrt{3}\pi$

• D.

  D. V = $\large 3\pi$

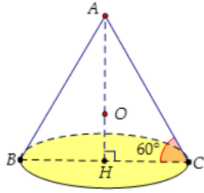
Gọi thiết diện qua trục là tam giác ABC như hình vẽ. Ta có:

$\large \widehat{ACB} = 60^{\circ} \Rightarrow \triangle$ABC đều. Đặt AB = a. Khi đó ABC là tam giác đều cạnh a

$\large \Rightarrow OH = r = \dfrac{a\sqrt{3}}{6}\Rightarrow a = \dfrac{6r}{\sqrt{3}}= \dfrac{6.1}{\sqrt{3}}= 2\sqrt{3}$ 

$\large \Rightarrow \begin{cases}
 & \ h = AH = \dfrac{a\sqrt{3}}{2} = \dfrac{2\sqrt{3}.\sqrt{3}}{2} = 3\\ 
 & \ R = \dfrac{BC}{2} = \dfrac{a}{2} = \dfrac{2\sqrt{3}}{2} = \sqrt{3}
\end{cases}$ 

Suy ra $\large V = \dfrac{1}{3}h\pi R^{2} = \dfrac{1}{3}.3\pi .(\sqrt{3})^{2} = 3\pi$