Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy bằng a . Kh

Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy bằng a. Khi đó mặt cầu nội tiếp hình chóp S.ABCD có bán kính bằng:

 

• A.

  A. $\large \dfrac{a(1+\sqrt{3})}{\sqrt{2}}$

• B.

  B. $\large \dfrac{a(\sqrt{6}-\sqrt{2})}{4}$

• C.

  C. $\large \dfrac{a(\sqrt{6}+\sqrt{2})}{4}$

• D.

  D. $\large \dfrac{a(\sqrt{3}-1)}{\sqrt{2}}$

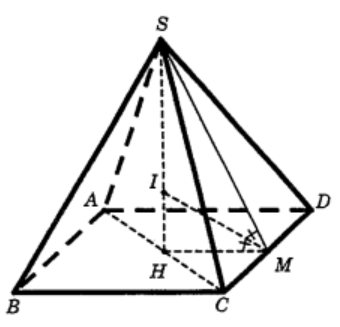
Gọi H là tâm của hình vuông ABCD. Ta có SH là trục đường tròn ngoại tiếp đáy. 

Gọi M là trung điểm của CD và I là chân đường phân giác trong của góc $\large \widehat{SMH} (I \in SH)$.

Suy ra I là tâm của mặt cầu nội tiếp hình chóp, bán kính r = IH.

Ta có $\large SH = \sqrt{SA^{2}-AH^{2}} = \dfrac{a\sqrt{2}}{2}$; 

$\large SM = \dfrac{a\sqrt{3}}{2}$ ; $\large MH = \dfrac{a}{2}$.

Dựa vào tính chất của đường phân giác ta có:

$\large \dfrac{IS}{IH} = \dfrac{MS}{MH} \Rightarrow \dfrac{SH}{IH} = \dfrac{MS+MH}{MH}$ 

$\large \Rightarrow IH = \dfrac{SH.MH}{MS+MH} = \dfrac{a}{\sqrt{2}+\sqrt{6}} = \dfrac{a(\sqrt{6}-\sqrt{2})}{4}$ 

Chọn B.