Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a . Mặt phẳng

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với đáy góc $\large 60^{\circ}$ và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A’B’C’ bằng:

• A.

  A. $\large \dfrac{85a}{108}$

• B.

  B. $\large \dfrac{3a}{2}$

• C.

  C. $\large \dfrac{3a}{4}$

• D.

  D. $\large \dfrac{31a}{36}$

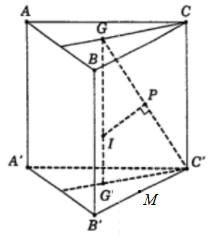
Gọi M là trung điểm B'C', ta có

$\large 60^{\circ} = (\widehat{(AB'C'),(A'B'C')}) = (\widehat{AM,A'M}) = \widehat{AMA'}$   

Trong $\large \Delta AA'M$, có $\large A'M = \dfrac{a\sqrt{3}}{2}$, suy ra $\large tan60^{0}=\dfrac{A'A}{A'M}\Rightarrow AA'=A'M.\sqrt{3}=\dfrac{3a}{2}$

Gọi G’ là trọng tâm tam giác đều A'B'C', suy ra G’ cũng là tâm đường tròn ngoại tiếp $\large \Delta A'B'C'$

Vì lăng trụ đứng nên $\large GG' \perp (A'B'C')$.

Do đó GG' là trục của tam giác A'B'C'.

Trong mặt phẳng (GC’G’), kẻ trung trực d của đoạn thẳng GC’ cắt GG’ tại I. Khi đó I là tâm mặt cầu ngoại tiếp khối chóp G.A’B’C’, bán kính R = GI.

Ta có $\large \Delta GPI \sim \Delta GG'C' \Rightarrow \dfrac{GP}{GI} = \dfrac{GG'}{GC'}$

$\large \Rightarrow R = GI = \dfrac{GP.GC'}{GG'} = \dfrac{GC'^{2}}{2GG'} = \dfrac{GG'^{2}+G'C'^{2}}{2GG'} = \dfrac{31a}{36}$ 

Chọn D.