Cho khối trụ có đáy là các đường tròn tâm ( O ), ( O’ ) có bán kính là

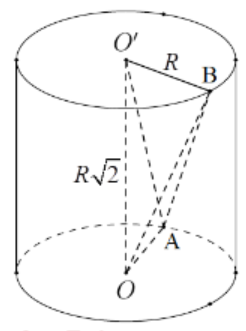
Cho khối trụ có đáy là các đường tròn tâm (O), (O’) có bán kính là R và chiều cao $\large h = R\sqrt{2}$. Gọi A, B lần lượt là các điểm thuộc (O) và (O’) sao cho OA vuông góc với O’B. Tỉ số thể tích của khối tứ diện OO’AB với thể tích khối trụ là:

• A. A. $\large \dfrac{2}{3\pi}$
• B. B. $\large \dfrac{1}{3\pi}$
• C. C. $\large \dfrac{1}{6\pi}$
• D. D. $\large \dfrac{1}{4\pi}$

Chọn C

Thể tích khối trụ $\large V_{1} = \pi R^{2}.h = \pi R^{2}.R\sqrt{2} = \pi R^{3}\sqrt{2}$.

Khối tứ diện BO’OA có BO’ là đường cao và đáy là tam giác vuông O’OA, do đó thể tích khối tứ diện là: 

$\large V_{2} = \dfrac{1}{3}S_{O'OA}.O'B = \dfrac{1}{3}.\dfrac{1}{2}OA.OO'.O'B = \dfrac{1}{6}R.R\sqrt{2}.R = \dfrac{\sqrt{2}}{6}R^{3}$ 

Vậy $\large \dfrac{V_{2}}{V_{1}} = \dfrac{R^{3}\sqrt{2}}{6}.\dfrac{1}{\pi R^{3}\sqrt{2}} = \dfrac{1}{6\pi}$.