Cho khối chóp S.ABCD có SA $\large \perp$(ABCD); đáy ABCD là hình than

Cho khối chóp S.ABCD có SA $\large \perp$(ABCD); đáy ABCD là hình thang vuông tại A và B với AB = BC = a; AD = 2a; SA = a. Gọi E là trung điểm của AD. Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ECD.

• A.

  A. $\large R = \dfrac{a\sqrt{7}}{2}$

• B.

  B. $\large R = a\sqrt{7}$

• C.

  C. $\large R = \dfrac{a\sqrt{11}}{2}$

• D.

  D. $\large R = a\sqrt{11}$

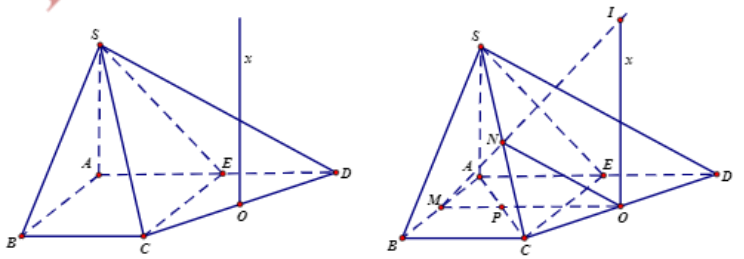
Gọi O là trung điểm của CD.

Kẻ tia Ox // SA thì Ox $\large \perp$(ABCD)

Ta có: O là tâm đường tròn ngoại tiếp tam giác vuông CDE và Ox $\large \perp$(ABCD), nên Ox là trục của đường tròn (CDE).

Gọi M, N lần lượt là trung điểm của AB, SC.

Ta có: $\large SM = \sqrt{SA^{2}+AM^{2}} = \dfrac{a\sqrt{5}}{2}$; 

$\large MC = \sqrt{MB^{2}+BC^{2}} = \dfrac{a\sqrt{5}}{2}$ nên suy ra SM = MC.

Do đó tam giác SMC cân tại M, suy ra MN $\large \perp$SC.

Dễ thấy (MNO) // (SAD) và CE $\large \perp$(SAD) nên suy ra CE $\large \perp$(MNO) và do đó CE $\large \perp$MN.

Vậy nên MN $\large \perp$(SEC), do đó MN là trục của đường tròn (SEC).

Gọi I là giao điểm của MN và Ox thì I chính là tâm mặt cầu ngoại tiếp hình chóp S.ECD.

Bán kính mặt cầu ngoại tiếp hình chóp S.ECD là $\large R = IC = \sqrt{IO^{2}+OC^{2}}$ .

Trong đó $\large OC = \dfrac{a\sqrt{2}}{2}$ và $\large IO = 3NP = 3.\dfrac{SA}{2} = \dfrac{3a}{2}$ (P là giao điểm của MO và AC).

Vậy thì $\large R = \sqrt{\left (\dfrac{a\sqrt{2}}{2}  \right )^{2} + \left (\dfrac{3a}{2}  \right )^{2}} = \dfrac{a\sqrt{11}}{2}$ 

Chọn C.