Một hình trụ có độ dài đường cao bằng 3, các đường tròn đáy lần lượt l

Một hình trụ có độ dài đường cao bằng 3, các đường tròn đáy lần lượt là (O;1) và (O’;1). Giả sử AB là đường kính cố định của (O;1) và MN là đường kính thay đổi trên (O’;1). Tìm giá trị lớn nhất $\large V_{max}$ của thể tích khối tứ diện ABMN.

• A.

  A. $\large V_{max} = 2$

• B.

  B. $\large V_{max} = 6$

• C.

  C. $\large V_{max} = \dfrac{1}{2}$

• D.

  D. $\large V_{max} = 1$

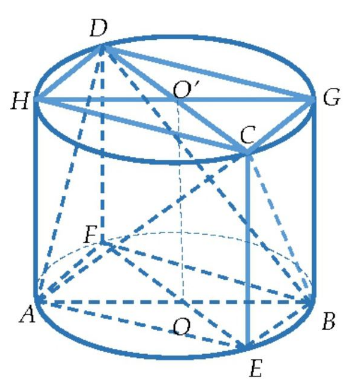
Dựng hình hộp chữ nhật AEBF.HCGD có thể tích V như hình vẽ.

Đặt $\large AF = x$, với $\large x\in (0;2)$ ta có $\large AE=\sqrt{AB^{2}-AF^{2}}=\sqrt{4-x^{2}}$.

Suy ra $\large V=AE.AF.AH=3x\sqrt{4-x^{2}}$

Thể tích khối tứ diện ABCD là $\large V_{ABCD}=\dfrac{V}{3}=x\sqrt{4-x^{2}}\leq \dfrac{x^{2}+4-x^{2}}{2}=2$ (BĐT Cauchy)

Dấu bằng xảy ra khi $\large x=\sqrt{4-x^{2}}\Leftrightarrow x=\sqrt{2}$

Vậy $\large V_{max}=2$  khi AEBF là hình vuông