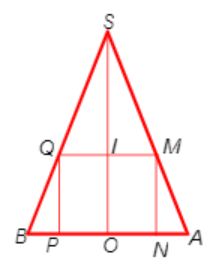
Cho hình vẽ bên. Tam giác SOA vuông tại O có MN // SO với M, N lần lượ

Cho hình vẽ bên. Tam giác SOA vuông tại O có MN // SO với M, N lần lượt nằm trên cạnh SA, OA. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN để thể tích khối trụ là lớn nhất.

• A.

  A. $\large MN = \dfrac{h}{2}$

• B.

  B. $\large MN = \dfrac{h}{3}$

• C.

  C. $\large MN = \dfrac{h}{4}$

• D.

  D. $\large MN = \dfrac{h}{6}$

Ta thấy khi quay quanh trục SO sẽ tạo nên một khối trụ nằm trong khối chóp. Khi đó thiết diện qua trục của hình trụ là hình chữ nhật MNPQ. 

Ta có SO = h; OA = R. Khi đó đặt OI = MN = x.

Theo định lý Thales ta có $\large \dfrac{IM}{OA} = \dfrac{SI}{SO} \Rightarrow IM = \dfrac{OA.SI}{SO} = \dfrac{R.(h-x)}{h}$ 

Thể tích khối trụ: $\large V = \pi IM^{2}.IO = \dfrac{\pi R^{2}}{h^{2}}.x(h-x)^{2}$ 

Áp dụng bất đẳng thức Cauchy ta có:

$\large 2x(h-x)^{2}\leq \left [ \dfrac{2x+2(h-x)}{3} \right ]^{3}$ 

Vậy $\large V \leq \dfrac{4\pi R^{2}h}{27}$. Dấu "=" xảy ra khi $\large x = \dfrac{h}{3}$. Hay $\large MN = \dfrac{h}{3}$ 

Chọn B