Với một miếng tôn hình tròn có bán kính bằng R = 6 cm . Người ta muốn
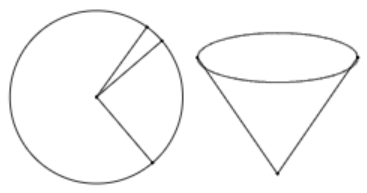
MỤC LỤC
Câu hỏi:
Với một miếng tôn hình tròn có bán kính bằng R = 6cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (Như hình vẽ)
Hình nón có thể tích lớn nhất khi người ta cắt cung tròn của hình quạt bằng:
Đáp án án đúng là: A
Lời giải chi tiết:
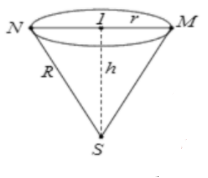
Gọi x, (x>0) là chiều dài cung tròn của phần được xếp làm hình nón.
Như vậy, bán kính R của hình tròn sẽ là đường sinh của hình nón và đường tròn đáy của hình nón sẽ có độ dài là x.
Bán kính r của đáy được xác định bởi đẳng thức 2πr=x⇒r=x2π
Chiều cao của hình nón tính theo Định lý Pitago là:
h=√R2−r2=√R2−x24π2
Thể tích khối nón:
V=13πr2h=13π(x2π)2√R2−x24π2
Áp dụng Bất đẳng thức Cauchy ta có:
V2=4π29.x28π2.x28π2.(R2−x24π2)
≤4π29(x28π2+x28π2+R2−x24π23)3=4π29.R627
Do đó V lớn nhất khi và chỉ khi:
x28π2=R2−x24π2⇔x=2π3R√6=2π36√6=4π√6.
Chọn A
Xem thêm các bài tiếp theo bên dưới
- Cho hình vẽ bên. Tam giác SOA vuông tại O có MN // SO với M, N lần lượ
- Cho khối chóp S.ABCD có SA ⊥(ABCD); đáy ABCD là hình than
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô
- Một cái thùng đựng đầy nước được tạo thành từ việc cắt mặt xung quanh
- Cho hàm số y=f(x) có bảng biến thiên như hình bên. Hàm số đã