Cho hình bình hành ABCD có $\large \widehat{BAD} = \alpha (0^{\circ} <
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình bình hành ABCD có ^BAD=α(0∘<α<90∘), AD = a và ^ADB=90∘. Quay ABCD quanh AB, ta được vật tròn xoay có thể tích là:
Đáp án án đúng là: C
Lời giải chi tiết:
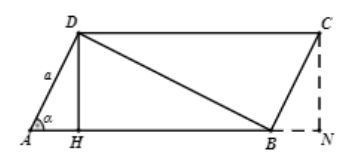
Kẻ DH⊥AB,CN⊥AB.
Các tam giác vuông HAD và NBC bằng nhau.
DH=CN=a.sinα
AH=BN=a.cosα
⇒HN=AB=acosα
Khi quay quanh AB, các tam giác vuông AHD và NBC tạo thành hai hình nón tròn bằng nhau nên:
V=13π.DH2.AH+(π.DH2.HN−13π.CN2.BN)
=π.DH2.AB=πa2.sin2α.acosα=πa3sin2αcosα
Chọn C
Xem thêm các bài tiếp theo bên dưới
- Trong các hình nón tròn xoay cùng có diện tích toàn phần bằng $\large
- Cho lăng trụ ABC.A’B’C’ , đáy ABC là tam giác có AB = 5, AC = 8 và góc
- Cho khối trụ có đáy là các đường tròn tâm ( O ), ( O’ ) có bán kính là
- Một hình trụ có độ dài đường cao bằng 3, các đường tròn đáy lần lượt l
- Với một miếng tôn hình tròn có bán kính bằng R = 6 cm . Người ta muốn